Genome-wide association studies
 Read with caution! This post was written during early stages of trying to understand a complex scientific problem, and we didn't get everything right. The original author no longer endorses the content of this post. It is being left online for historical reasons, but read at your own risk. |
Genome-wide association studies (GWAS) are where you take genome-wide (i.e. not targeted to a particular locus) genetic data — and this could be SNPs, whole exome or whole genome — for a large number of individuals and you look for variants that are significantly correlated with a particular phenotype of interest.
A few different scientists have given me the 15-second overview of the history of GWAS as they see it. Which goes something like this: there was a big trendy wave of GWAS in the mid-2000s which identified a lot of common, small-effect-size variants contributing to relatively common diseases (the things people refer to as genetic “risk factors” for things like heart attacks, Alzheimer’s, Parkinson’s, etc) and then the wave died down and by 2012 GWAS are considered to be bread-and-butter or even a bit passe. (I am still waiting to hear a clear articulation of why on this last point).
In any event, GWAS are definitely still going on, and although there has been a lot of publicity for GWAS dealing with risk factors for common diseases, there have also been GWAS addressing modifiers for rare diseases, with potentially interesting findings for both prion diseases and Huntington’s. I will review a few such studies a bit later in this post, but first, I’m going to write up what I learned from a couple of large, prestigiously-published reviews of the overall field of GWAS. Manolio 2010 (NEJM) and McCarthy 2008 (Nature) both provide nice overviews of how GWAS work and the many issues and challenges associated with them, both in terms of study design and modeling methodologies.
McCarthy begins his discussion of GWA study design with the twin issues of case and control selection. Implicit is the assumption that GWAS are always dichotomous case-control comparisons. Does it need to be that way? Plenty of disease phenotypes are quantifiable, whether objectively (say, age of onset of a disease) or subjectively (say, clinical rating of disease severity). But so far I have run across no evidence of anyone doing a GWAS with a continuous (rather than binary) dependent variable. In any event, there are a number of tricky issues associated with control selection. Here are a few different ways to choose controls:
- Population-based controls. i.e., people from the general population. You can’t guarantee none of them also have the disease, so you need a particularly large sample size to detect the genetic differences between them and your cases.
- Regular old controls. Just people who don’t have the disease.
- Hypernormal controls. People who really, really don’t have the disease. For instance, in the study of kuru, elderly people who had been exposed to kuru yet survived were considered hypernormal controls. Hypernormal controls give you a lot of statistical power at small sample sizes, but sometimes leave you open to bias. McCarthy gives a good example of this: “selecting extremely low-weight individuals as controls for a case-control study of obesity could result in overrepresentation of alleles primarily associated with chronic medical disease or nicotine addiction rather than weight regulation.”
Population-based controls are temptingly easy to get– you just need any random people who’ve been genotyped, so some studies use existing data sources (1000 Genomes, HapMap, etc.) as their controls. Other studies use a common pool of controls for studies against several different case groups for different diseases. But as soon as you take these sorts of shortcuts you run into a few big problems.
First, there may be technical differences between the samples. The control data was probably gathered in a different way, in a different year, at a different facility than the case data. Different gene chips, sequencing equipment, DNA format (whole genome or called?), software used to reconstruct the sequence from shotgun segments, etc. can all create some amount of systemic error. If the case and control datasets have different systemic errors, you’ll find all sorts of false positive associations.
Second, there may be differences in population. As one obvious example, a lot of diseases are associated with people of a particular ethnicity. If your cases are mostly or entirely of that ethnicity and the controls are of a different ethnicity, then any variant associated with this ethnic difference will show up as significant in your study. But this issue is not limited to what you might think of as “ethnic groups” in the common sense; smaller sub-ethnic groups, clans or families will also complicate the study. McCarthy defines two useful terms which he groups under the heading of “latent population substructure”:
Population stratification. The presence in study samples of individuals with different ancestral and demographic histories: if cases and controls differ with respect to these features, markers that are informative for them might be confounded with disease status and lead to spurious associations.
Cryptic relatedness. Evidence — typically gained from analysis of GWA data — that, despite allowance for known family relationships, individuals in the study sample have residual, non-trivial degrees of relatedness, which can violate the independence assumptions of standard statistical techniques.
I opened up Gayan 2008 ”Genomewide Linkage Scan Reveals Novel Loci Modifying Age of Onset of Huntington’s Disease in the Venezuelan HD Kindreds” expecting to read a paper about early and late disease onset modifiers for HD. Though that is the paper’s purpose, I was shocked to find that the plurality of the text was actually devoted to explaining how Gayan modeled and analyzed the family relationships in the case sample. Perhaps this issue was of unusually high importance in this paper because the majority of Gayan’s cases came from one very large Venezuelan kindred. Still, I marveled at the complexity that had to be addressed. Researchers had collected stated family relationships from the case patients in interviews, but the researchers still then validated these stated relationships by analyzing the SNP data, finding discrepancies such as 23 non-paternities. Once they’d corrected and validated the pedigree, the researchers wanted to model all of the family relationships in their data.
The goal of this modeling was to control for linkage disequilibrium. As best I can tell, this is simply the observation that variants don’t independently assort. We know that genes physically near one another on the same chromosome tend to be inherited together because there is little room for crossover; but there are plenty of reasons why even genes at distant loci or on different chromosomes would wind up in disequilibrium. Wikipedia lists a few such reasons:
The level of linkage disequilibrium is influenced by a number of factors, including genetic linkage, selection, the rate of recombination, the rate of mutation, genetic drift, non-random mating, and population structure.
So in the case of Gayan’s Venezuelan kindreds, I can imagine a couple of issues. If one family tends to have early HD onset and another has late HD onset, SNPs common to one family and not the other will show up as associated even if they are not causal. Another issue is that because so many of the case patients are closely related to one another, there haven’t been a lot of generations for crossover to occur, so variants that were co-located on one allele in a common ancestor will be likely to still be co-located in the descendants. Then if one gene on this allele is actually functionally correlated with age of HD onset, all the genes near it will also appear to be. Gayan uses a piece of software called Merlin to model the linkage disequilibrium, but even then, apparently modeling all the family relationships in a 10-generation family is too computationally intensive, so much of the paper is devoted to discussing the tradeoffs and sacrifices made in order to get something computationally tractable.
This discussion of case and control selection has by now gotten into some of the statistical issues with GWAS in general. I mentioned earlier that it’s good to have the sequencing technology be uniform across case and control. But even if you do that, sequencing technology isn’t perfect, and some SNPs or some regions of the exome or genome will have higher coverage or higher call quality than others. There is a tendency for these regions of low data integrity to show up disproportionately as significantly associated with phenotype. So in setting the threshold for what’s considered valid data, you end up with another type 1 / type 2 error tradeoff. Similarly with linkage disequilibrium: when a SNP is found to be far out of Hardy-Weinberg Equilibrium (HWE), that can indicate technical errors, and so there is a tendency to toss out such SNPs, and yet being out of HWE can also be a genuine indicator that a variant really is associated with phenotype.
Correlation doesn’t imply causation, and all of these linkage disequilibrium issues are specific manifestations of that. Yet I had always figured that in genetics, at least you know that the phenotype doesn’t cause the genotype. But even this can be turned on its head a bit by the concept of informative missingness. Allen writes:
Parental data can be informatively missing when the probability of a parent being available for study is related to that parent’s genotype; when this occurs, the distribution of genotypes among observed parents is not representative of the distribution of genotypes among the missing parents. Many previously proposed procedures that allow for missing parental data assume that these distributions are the same. We propose association tests that behave well when parental data are informatively missing, under the assumption that, for a given trio of paternal, maternal, and affected offspring genotypes, the genotypes of the parents and the sex of the missing parents, but not the genotype of the affected offspring, can affect parental missingness.
While Allen is referring to a genuine genotype-phenotype association that might be missed by a naive statistical model, McCarthy seems to use the term rather differently, to refer to a situation where an association is falsely implied by bad data:
Informative missingness. If patterns of missing data are nonrandom with respect to both genotype and trait status, then analysis of the available genotypes can result in misleading associations where none truly exists.
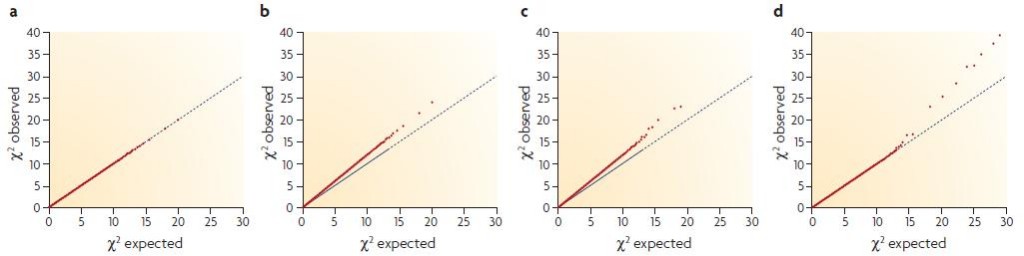
An impressive tool that McCarthy has introduced me to is the quantile-quantile plot, which offers a trip into the meta world of statistics about statistics. Consider this: if you look at 20,000 variants, then on expectation, 200 of them will be significant at the p < .01 threshold even if none are actually biologically relevant. Therefore, if you find that 400 are significant at the .01 threshold, then something funny is going on. In other kinds of studies this could itself be a good and interesting result: suppose you’re analyzing a featurized space of financial transactions or ad clicks; the fact that some “extra” features look significant could suggest that your data do have predictive value and you’ll be able to build a useful model. But in GWAS, this sort of finding usually means you’ve got some sort of problem on your hands: perhaps you didn’t model the family or ethnic differences in the samples well enough and so all manner of genes that are simply associated with a family or ethnic group are coming up as associated with the disease. The Q-Q plot helps to illuminate this sort of problem. Here are McCarthy’s examples:
(a) is a valid model finding no associated variants– no more of them appear statistically significant than would be expected given the large number of questions asked. (b) is a problematic model showing associated variants: the fact that the red dots are categorically above the diagonal axis shows an elevated amount of statistical significance for a huge number of variants, which is probably the result of population stratification. (d) is what you hope for in a GWAS: the data are well-behaved in that for the vast majority of variants there is no more statistical significance than would be randomly expected, but for a handful of variants (in this case, about 8) there is vastly elevated significance, indicating these variants actually are associated with the disease.
GWAS are never conclusive on their own; McCarthy devotes much discussion to the ways in which a finding must be followed up. If you find something significant and relevant, first you’ll want to do a technical replicate to make sure your data were accurately collected. Next you (or some other researcher) will want to find a whole separate case/control group and see if your results can be duplicated in this different population. What’s tricky is, if the results are not duplicated, that doesn’t always mean you were wrong– you could be wrong, or it could just be that the different population chosen for the follow-up study has different allele frequencies and so the effect is not observable, or that the studies were designed a bit differently. McCarthy gives a great example for this last case:
A recent example is provided by the highly significant association between variants in the fat mass and obesity associated (FTO) gene and type 2 diabetes that was first detected in a UK GWA scan (odds ratio for diabetes ~1.27, p = 2 x 10–8) and subsequently strongly replicated in other UK samples (odds ratio for diabetes ~1.22, p = 5 x 10–7). However, this association could not be replicated in several wellpowered diabetes GWA scans. The explanation for these divergent findings derives from the fact that FTO was shown to influence diabetes risk through a primary effect on weight regulation, such that the diabetes risk allele is associated with higher fat mass, weight and body mass index. In the UK studies, marked differences in weight between diabetic cases and non-diabetic controls meant that differences in FTO genotype frequencies were observed in diabetes case–control analyses. Several other diabetes GWA scans had explicitly targeted case selection on relatively lean individuals (to remove the confounding effects of obesity), thereby abolishing the differences in weight between the diabetic cases and controls, and with it the between-group differences in FTO genotype distributions. Rather than dismissing the FTO association with type 2 diabetes as a failure of replication, identification of the source of the heterogeneity (what might be termed informative heterogeneity) provided an explanation for the discrepant findings and highlighted the likely mechanism of its action.
Given the huge number of factors to control for and the huge potential for false positives in GWAS, McCarthy notes that one trend is towards Bayesian statistics incorporating known biology into the model. Acknowledging that 200 of 20,000 variants will show up significant even if they’re not actually, this approach seeks to vet the 200 significant variants by how biologically likely the result seems. For genes known to interact with a disease-relevant gene or to be co-regulated or to be part of the same pathway, you assign a higher prior probability than for genes you’d be very surprised to find relevant. This is a useful tool, though unfortunately much of the “data” we have on pathways and interactions is based on literature searches rather than directly, objectively measured data, and this whole approach makes it harder to find those rare things that are surprising-yet-true.
Manolio 2010 provides a different sort of overview of GWAS, abstracted a bit more from the study design and methodology and focusing more on the implications of GWAS findings. Particularly interesting was the note that most GWAS have only been able to account for a small fraction of the heritable portion of variance in disease susceptibility, and Manolio’s discussion about some possible reasons for this:
These studies raise many questions, such as why the identified variants have low associated risks and account for so little heritability. Explanations for this apparent gap are being sought. Perhaps the answer will reside in rare variants… which are not captured by current genomewide association studies; structural variants, which are poorly captured by current studies; other forms of genomic variation; or interactions between genes or between genes and environmental factors.
The point about rare variants is interesting– I wonder if some of the disease susceptibility has to do with the rare loss-of-function variants that Daniel MacArthur studies. The rest of Manolio’s paper was a nice backgrounder on what’s been achieved (as of 2010) by GWAS, which I’d recommend, as well as a discussion of the clinical implications of GWAS, particularly the issue of how these low-odds-ratio genetic risk factors should be framed to patients and whether and how it should impact what kind of care and screening they receive. This part was interesting too and introduced me to a new concept for interpreting risk: “area under the receiver-operating-characteristic curve (AUC)”.
So let’s move on to a discussion of GWAS as it pertains to rare diseases. Even though we’ve known the genetic basis for Fatal Familial Insomnia since Medori 1992 and for HD since MacDonald 1993, there is still a lot that GWAS could tell us about these diseases. Both have wide variance in age of onset, and in the case of HD, it’s been well established that much of that variance is familial, whether due to genetic or shared environmental factors. For both diseases, it would be really useful to identify genetic variants which accelerate or decelerate disease onset, for several reasons:
- It would give us clues to the pathways that PrP/Htt are involved in and thus help us to understand the protein’s native function.
- There might already exist approved drugs which interfere in those pathways or interact with the protein products of the genes in which variants are found. These drugs would be prime candidates to test as therapeutics.
- If we can figure out the structure of the active site on the implicated proteins, perhaps we could design a drug that mimics their effect (see the story of how tafamidis was invented).
Lukic & Mead 2011 provide a nice review of the several prion disease GWAS that have been completed to date. Only 15% of prion disease cases are (known) genetic cases, with the remainder either sporadic or variant. But there are likely to be genetic determinants even for susceptibility to sporadic or variant prion diseases as well. Lukic writes: “Familial concurrence of sporadic CJD has been observed in the absence of a causal mutation.” (citing Webb 2008, a case of two siblings) and we also know of the strange case of sFI in an FFI family. Moreover, with regards to variant CJD Lukic writes:
The strongest genetic association of a common genotype with any disease has been observed in variant CJD. All patients with neuropathologically proven variant CJD have been homozygous for methionine at polymorphic codon 129 of the prion protein gene (PRNP). Homozygous genotypes at codon 129 also strongly associate with sporadic CJD, iatrogenic CJD and early age of onset of inherited prion disease (IPD), and kuru. Although this is a powerful effect, about a third of the population exposed to BSE are homozygous for methionine at PRNP codon 129, while only around 220 individuals have developed vCJD to date, implicating the potential important role of other susceptibility loci.
Lukic mentions a couple of variants which are known to modify prion disease, which I wasn’t aware of– “Another genotype, heterozygosity at codon 219, commonly found in several Asian populations, has been shown to be protective against sporadic CJD but is neutral or may even confer susceptibility to vCJD” (citing Lukic 2010 in Neurology and Shibuya 2004), and also the fact that there are non-coding variants of PRNP which have been shown associated (whether positively or negatively) with the disease. This last point makes sense in light of what Jeffery Kelly said about protein concentrations (see tafamidis post)– perhaps these non-coding variants are in promoter regions or somehow impact expression levels.
Lukic then reviews the results of a U.K.-based GWAS for vCJD susceptibility which found risk loci just upstream of RARB, a kuru study which found an association with STMN2, a mouse model study implicating HECTD2, and a study of sCJD and vCJD implicating SPRN which codes for Shadoo or Sho, meaning Shadow of PrP. It seems that at this point all of these loci are fairly speculative and will need to await replication in other studies before we have any confidence of a genuine association with prion disease.
I also found one other citation on GWAS for prion diseases, Lloyd 2010, but was not able to locate the article.
For HD it seems there’s been a great deal more work done, though unfortunately it’s not clear that we have better answers. The HD GWAS I found were looking at what genes modify age of onset, which is highly variable and heritable in HD. As Gayan 2008 explains:
over 90% of individuals worldwide, have between 40 and 50 CAG repeats. For these individuals, the number of CAGs only accounts for approximately 44% of the variability in age of onset [Wexler et al., 2004]. People with 44 CAGs, for example, can vary as much as 20 years or more in age of onset, even within the same family. This variability in age of onset not explained by the size of the CAG repeat is called the residual age of onset. We have demonstrated that the residual age of onset is itself highly heritable, with heritability estimates of 40–80% [Wexler et al., 2004].
Gayan’s dataset is 443 cases and 360 controls. The controls were drawn from the same families as the cases, just from the individuals without lengthy enough expanded CAG repeats to have HD. Only about SNPs are examined, and only about 6,000 of them, since the work was done in 2007. As I discussed above, much of the text of the paper deals with validating the data and modeling the linkage disequilibrium due to the familial relations of all the individuals involved. Somehow, nowhere does the paper make very clear, to my eye at least, exactly what model was used to analyze the SNPs– are they modeling residual age of onset as a continuous variable, or is there a dichotomous “early” vs. “late” comparison? The paper finds several loci significantly associated with HD age at onset, with the highest one having a logarithm of odds ratio (LOD) of 4.29. I am not clear if the authors are referring to all of their results or only a subset thereof when they write that “After correction for multiple testing, none of the association results at the SNPs within the linkage curves were statistically significant.” Most curiously to me, the SNPs are all referred to by location on chromosome rather than by gene that they are in or near. Had so many genes not yet been annotated when this study was done? There is discussion of linkage peaks and the idea that the actual gene of interest might be between the measured SNPs. Perhaps the goal of this study, given the technological limitations of its day, was simply to identify candidate locations on a chromosome where associated variants might lie, rather than to identify the variants themselves.
I also dug up an even earlier GWAS for Huntington’s disease, Andresen 2007. This study uses targeted probes to sequence just a few portions of the genome, for approximately the same Venezuelan study participants as Gayan used — 443 cases and 361 controls. The goal is to replicate the findings of earlier studies which had identified twelve variants as being associated with HD age of onset. The original studies were from the U.K., India, and Germany, so the Venezuelan dataset offered a chance to replicate those findings with a different population. Only 1 of the 12 variants passed muster for replication. Now, that doesn’t mean the original studies were wrong, for various reasons that McCarthy 2008 describes. Indeed, for one of them, GRIK2, Andresen notes that the allele frequency is too low in Venezuela to obtain statistical significance, even though the effect may well be present, a good example of the allele frequency issues in replication that McCarthy discusses. The one gene that does meet standards for replication in Andresen’s study is GRIN2A, and moreover, this gene also makes biological sense:
GRIN2A encodes the NR2A subunit of the NMDA-type glutamate receptor. This subunit is expressed on the striatal medium spiny neurone, the cell type that is most prone to degeneration in Huntington’s disease. These cells also seem to be particularly sensitive to glutamate excitotoxicity, as injection of quinolinic acid (an excitotoxic agent) into the striatum of rodents or primates causes the same neurones to die, resulting in a Huntington’s disease-like syndrome. Variation in function or expression of glutamate receptor subunits could modulate excitotoxic death and affect the age of onset.
Which is another good example of McCarthy’s theme of biological relevance playing a role in our interpretation of GWAS findings. Unfortunately I haven’t been able to find any GWAS work on HD more reecnt than 2008.