Power for GWAS and extreme phenotype studies
Motivation
Today many researchers are simultaneously pursuing ever-larger genome-wide association studies (GWAS) using SNP chips, while also pursuing exome sequencing studies to try to find rarer variants than can be found in GWAS. Rare variants are less likely to be well-tagged by GWAS SNPs, so it’s believed that exome sequencing will have better power for rare variants, though as of today there are precious few examples of significant associations being found (one still-debated example is Emond’s cystic fibrosis study).
GWAS have poorer power to detect rare variants per individual genotyped, but at $50 or $100 per chip you can genotype a lot of people. Exome sequencing still costs several hundred dollars, and inevitably exome studies are much smaller than GWAS.
In terms of strategic planning, then, an important question is: “how many people do I need to include in my exome study in order to have power to detect something I won’t already find anyway through my GWAS?”
This post aims to show how to answer this question. Since I work on Huntington’s Disease age of onset, I’ll present the issue in that light. First, here is some background information.
Background on quantitative phenotypes and models
Much of the literature on association studies deals with case/control studies. ”Quantitative” here is the opposite of “case/control”. Quantitative means continuous as opposed to discrete; numeric as opposed to binary or dichotomous. For instance, LDL levels which vary continuously from ~25 to ~200 are a quantitative phenotype, while “people with schizophrenia” vs. “people who don’t have schizophrenia” is a case/control phenotype.
HD residual age of onset is an intrinsically quantitative phenotype and deserves slightly different treatment than many other phenotypes. Some other studies of quantitative phenotypes still speak of an odds ratio or other such terminology really intended for dichotomous case/control comparisons. They do that because for many quantitative phenotypes such as blood lipid levels, clinicians still have some cutoff they use to decide when a person is “affected” and an intervention is needed. Other times the phenotype starts out dichotomous and researchers then subtract out effects of non-genetic factors to get a “liability” score (see Guey 2011 for an example). But all of the HD patients are affected, it’s just a matter of when. There is no meaningful cutoff. So instead of odds ratios, effect sizes are better thought of in terms of years or standard deviations.
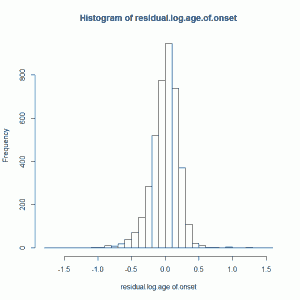
HD residual (log) age of onset is created by subtracting predicted log age of onset (predicted based on CAG length, which controls ~70% of variance in overall HD age of onset) from actual log age of onset. This gives you a residual which is uncorrelated with CAG length. This residual looks vaguely normally distributed, though it’s skewed a bit left (i.e. the mean is left of the median) and is way excessively kurtotic (leptokurtic to be fancy), with a kurtosis of about 5.3 using kurtosis() from the R fBasics package):
For a moment I’ll just assume this is normal anyway (I’ll un-assume this later) and I’ll z-score it, so that I’m using a standardized residual log age of onset.
As mentioned previously, we think that ~40% of the variance in this residual is heritable [U.S.-Venezuela Collaborative Research Project 2003] and our goal is to find the genetic variations that make up that heritability.
One simple way to model the effect of a hypothetical causal variant is to assume there’s an underlying normal distribution of phenotypes with an effect due to the causal variant “spiked in”. The causal variant has a given frequency we’ll call maf, and an effect size we’ll call es. It’s random whether any person gets a causal variant, but if they do, then it adds its effect size to their phenotype. Here’s an example in R for a hypothetical causal SNP with frequency 3% and effect size equal to 0.6 standard deviations:
N = 6000
maf = .03
es = .6
allele_counts = rbinom(n=N,prob=maf,size=2) # size=2 because we're diploid
phenotypes = rnorm(n=N,m=0,sd=1) + es*allele_counts
Note that maf and effect size together will determine the proportion of overall variance explained by the variant. Variance explained in the population is approximately equal to (es)2*maf. For the above example, it should be about (.6)2*.03 = .0108, i.e. about 1% of variance explained. If you actually run the above code and do a linear model lm(phenotypes~allele_counts) you’ll tend to get a smaller number because this is just a model of a small sample, but if you pick much bigger numbers to simulate “the population” you’ll get something fairly close – try this:
ph = c(rnorm(970000,m=0,sd=1),rnorm(30000,m=.6,sd=1))
ge = c(rep(0,970000),rep(1,30000))
summary(lm(ph~ge))
(Admittedly a simplification ignoring homozygous individuals). But I get .0104, which is pretty close to .0108.
Now here I’ve already started doing linear models. That’s one way to associate phenotype with genotype, supported by the PLINK --linear feature and easy to do in R, and Dupont 1998 discusses how to calculate power for this model, though not specifically in a genetic context. Perhaps more widely used in genetic association studies is the likelihood ratio test. To review, this consists of the following:
La is the likelihood of the given data under an alternative hypothesis (i.e. “this SNP has an effect”, with the effect size estimated based on the data)
L0 is the likelihood of the given data under the null hypothesis (“this SNP has no effect”)
D = 2(ln(La)-ln(L0))
D is the likelihood ratio test statistic. Compare it to the chi-squared distribution with degrees of freedom dfa – df0 in order to determine a p value.
A formulation which is only slightly different is the Wald test, which computes D from the model parameters rather than likelihood.
θa = maximum likelihood estimate of model parameter
θ0 = model parameter under the null
D = (θa – θ0)2 / var(θa)
And as above, D is compared to the chi-squared distribution.
The likelihood ratio and Wald tests are asymptotically equivalent. If you’ve ever used PLINK’s --assoc feature with a quantitative phenotype, it assumes asymptotic behavior and so is using either/both of these. If you aren’t sure that your data meet asymptotic assumptions, you can use max(T) permutation with the --mperm command, and that uses the likelihood ratio test.
It seems people are using both likelihood ratio and/or linear models in the literature for quantitative trait loci (QTLs, i.e. variants that impact quantitative phenotypes). As one example, Melzer 2008 does initial association using linear models in PLINK but then validates the most significant SNPs with permutation using max(T) permutation, thus the likelihood ratio test.
How to compute power for a GWAS on a quantitative phenotype
You could imagine simulating power for a GWAS linear model by creating the normally distributed phenotype and spiking in effect size as I’ve done above, running a linear model, and repeating 100 or 1000 times to see how often the coefficient for your SNP has a p value less than the threshold you want. But hold on there, a power calculation for GWAS is not quite that straightforward. Say our array has a million SNPs on it; it might happen to include the causal SNP, or it might just include a bunch of SNPs that are close enough to the causal SNP to be in linkage disequilibrium (LD). So you have to consider the extent of LD, and then not only the minor allele frequency of the causal SNP but also the “marker” SNP that might end up being a proxy for it.
I looked on the web for some guidance as to what assumptions I can make about LD if you assume, say, ~1M SNPs on a chip (thus an average of 1 SNP per 3000 bases). The answer: it’s really complicated. Eberle 2006 separately analyzes groups of unrelated Europeans, Africans and Asians and presents a nice graph of how LD between two common SNPs decays as the SNPs get further apart, depending on whether or not you only look at frequency-matched SNPs. Spencer 2009 argues that LD patterns in the human genome are too complex for there to be any closed-form solution for calculating power for GWAS: instead it can only be done by simulation. Spencer presents the HAPGEN and GWAPOWER R packages for doing these simulations, but they only work for case/control studies whereas I’m dealing with quantitative phenotype.
Any power calculation will rest on a variety of assumptions, so I decided I’m willing to accept some assumptions about LD for now, knowing that I can vary that assumption and see how power is affected. To get started, let’s do some back-of-the-envelope here. If the 1M SNPs are uniformly scattered across the genome, they occur every 3kb and so the farthest that one ungenotyped SNP can get from its nearest genotyped SNP is 1.5kb. And to the extent that the SNPs aren’t uniformly scattered, it’s probably because they’re concentrated in regions of functional importance and sequence conservation, so it’s not clear that power is actually reduced. Eberle’s graphs are on the scale of 200kb; if you squint your eyes to see what’s going on at 1.5kb, LD is up around 90% of theoretical maximum. That’s for common SNPs (> 10%); Eberle is also looking at frequency-matched SNPs but my understanding is that this is accounted for if you use D’, which is adjusted for frequency. I decided to start by assuming LD of 0.8 between a theoretical causal SNP and its nearest marker.
I asked around for what tools people use to calculate power for GWAS, and I learned that Shaun Purcell’s GPC is the most widely used tool for calculating power for association studies. It’s really stood the test of time, having been launched in 2002, which is ancient history in bioinformatics time. It can calculate power for a number of different types of studies; the QTL association feature works for quantitative phenotypes. This feature calculates power based on a likelihood ratio test - Purcell 2003 cites Sham 2000 for the method.
GPC is much more elegant and straightforward than the deluge of similar tools that have come out since it was first released. I’m interested in calculating power for a variety of different effect sizes and minor allele frequencies and creating a sort of “heat map” of what sort of variants we are powered to detect in our GWAS. GPC has no web service so this would require a lot of clicking back and forth. I also, after reading Sham 2000, couldn’t wrap my head around the method GPC is using and why it didn’t match results I was getting in a simpler simulation. Motivated by the desire to automate this process as well as my desire to understand any tool I’m going to use rather than just black boxing it, I got in touch with Shaun Purcell, who was nice enough to share the source code for the QTL association feature with me so I could port it to R. Here’s my R implementation along with a few tests you can check against GPC itself to see that you get the same result:
# Eric Minikel - CureFFI.org
# 2012-12-05
# R implementation of QTL association as featured in Genetic Power Calculator:
# http://pngu.mgh.harvard.edu/~purcell/gpc/
# based on C++ source code generously provided by Shaun Purcell
# who in turn based it on method in Sham 2000:
# http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1378020/
likelihood.ratio.test.power = function(alpha,df,ncp) {
return ( 1-pchisq(q=qchisq(p=1-alpha,df=df,ncp=0),df=df,ncp=ncp) )
}
# qtl.assoc.power
# calculates power for specified n
# parameters, their names in GPC, and explanations:
# n = Sample Size
# vq = Total QTL Variance = fraction of trait variance explained by this SNP
# p = QTL increaser allele frequency = MAF of causal SNP
# m1 = Marker M1 allele frequency = MAF of marker SNP, proxy for causal SNP
# dprime = Linkage disequilibrium (D-prime)
# alpha = User-defined type I error rate
# da = Dominance : additive QTL effects = set nodom=FALSE to use this
# nodom = No dominance = flag to ignore da and assume purely allelic model
# parent = Both parents genotyped = flag for whether parents are included
# sibr = Sibling correlation
# s = Sibship Size = 1 for unrelated individuals, 2 for sib pairs, etc.
# whichpower = which power calc you want: "overall", "between", "within"
# for more details see notes: http://pngu.mgh.harvard.edu/~purcell/gpc/#qtl_ins
qtl.assoc.power = function(n,vq,p,m1,dprime,alpha,da=0,nodom=TRUE,parent=FALSE,sibr=1,s=1,whichpower="overall") {
if(nodom) {
tdf = 1 # 1 degree of freedom without dominance
# allele count is assumed to be linear with effect, so the only thing
# that can vary is the slope
} else {
tdf = 2 # 2 degrees of freedom with dominance
# allele counts 0, 1, 2 vs. their effects are not collinear
}
# allele frequencies
q = 1 - p # major AF of causal SNP
m2 = 1 - m1 # major AF of marker SNP
# recover un-normalized linkage disequilibrium
# back-calculate regular D based on D' which is passed to this function
# see http://en.wikipedia.org/wiki/Linkage_disequilibrium#Definition
dmax = p*m2
if (q*m1 < dmax) {
dmax = q*m1
}
ld = dprime * dmax
# calculate haplotype frequencies
h00 = p*m1 + ld # based on D from above, get haplotype frequencies
h01 = p*m2 - ld
h10 = q*m1 - ld
h11 = q*m2 + ld
# genetic values
vtot = 1
a = sqrt( (vq*vtot) / ( (2*p*q)*(1+da*(q-p))**2 + (2*p*q*da)**2 ) )
d = da*a
# variance components
va = 2 * p * q * ( a + d*(q-p))**2
vd = (2*p*q*d)*(2*p*q*d)
vs = sibr*vtot - va/2 - vd/4
vn = (1-sibr)*vtot - va/2 - 3*vd/4
# attenuation factor due to incomplete LD for association test
phisq = ((h00 - m1*p)**2/(m1*p))
phisq = phisq + ((h10 - m1*q)**2/(m1*q))
phisq = phisq + ((h01 - m2*p)**2/(m2*p))
phisq = phisq + ((h11 - m2*q)**2/(m2*q))
vam = phisq * va
vdm = phisq**2 * vd
vsm = vs + (((1-phisq)*va)/2) + (((1-phisq**2)*vd)/4)
vnm = vn + (((1-phisq)*va)/2) + ((3*(1-phisq**2)*vd)/4)
# compute expected non-centrality parameters
# ncp_b = between sibships
# ncp_w = within sibships
if (parent) {
ncp_b = log(vnm + s*vsm + (s/2)*vam + (s/4)*vdm) - log(vnm + s*vsm)
ncp_w = log((vnm+0.5*vam+0.75*vdm)**(s-1)) -
log(vnm**(s-1)) +
log(vnm + s*vsm + 0.5*vam + 0.75*vdm) -
log(vnm + s*vsm)
} else {
ncp_b = log(vnm + s*vsm + ((s+1)/2)*vam + ((s+3)/4)*vdm) -
log(vnm + s*vsm)
ncp_w = log((vnm + 0.5*vam + 0.75*vdm)**(s-1))-log(vnm**(s-1))
}
# take sample size into account
ncp_b = ncp_b * n
ncp_w = ncp_w * n
between.sibships.power = likelihood.ratio.test.power(alpha,tdf,ncp_b)
within.sibships.power = likelihood.ratio.test.power(alpha,tdf,ncp_w)
overall.power = likelihood.ratio.test.power(alpha,tdf,ncp_b+ncp_w)
if (whichpower == "overall") {
return(overall.power)
} else if (whichpower == "between") {
return(between.sibships.power)
} else if (whichpower == "within") {
return(within.sibships.power)
} else {
stop(paste("invalid whichvalue parameter:",whichpower))
}
}
# a few tests
qtl.assoc.power(n=6000,vq=.01,p=.01,m1=.01,dprime=.8,alpha=5e-08)
qtl.assoc.power(n=6000,vq=.001,p=.01,m1=.01,dprime=.8,alpha=5e-08)
qtl.assoc.power(n=6000,vq=.01,p=.01,m1=.01,dprime=.8,alpha=5e-08,sibr=.5,s=2)
qtl.assoc.power(n=6000,vq=.01,p=.01,m1=.01,dprime=.8,alpha=5e-08,sibr=.5,s=2,parent=TRUE)
qtl.assoc.power(n=6000,vq=.01,p=.01,m1=.01,dprime=.8,alpha=5e-08,sibr=.5,s=2,parent=TRUE,nodom=FALSE,da=0.5,whichpower="between")
qtl.assoc.power(n=6000,vq=.01,p=.01,m1=.01,dprime=.8,alpha=5e-08,sibr=.5,s=2,parent=TRUE,nodom=FALSE,da=0.5,whichpower="within")
qtl.assoc.power(n=6000,vq=.01,p=.01,m1=.01,dprime=.8,alpha=5e-08,sibr=.5,s=2,parent=TRUE,nodom=FALSE,da=0.5,whichpower="overall")
You’ll notice that the GPC (and thus this code) expects “Total QTL variance” as one of its inputs (vq). This is the proportion of phenotypic variance explained by the putative causal variant (basically an R2). To me, that’s a bit non-intuitive: I’d rather think of R2 as a dependent variable that’s a function of allele frequency and effect size. If you’re assuming normality and expressing effect sizes in standard deviations, then you can calculate vq = es2*maf.
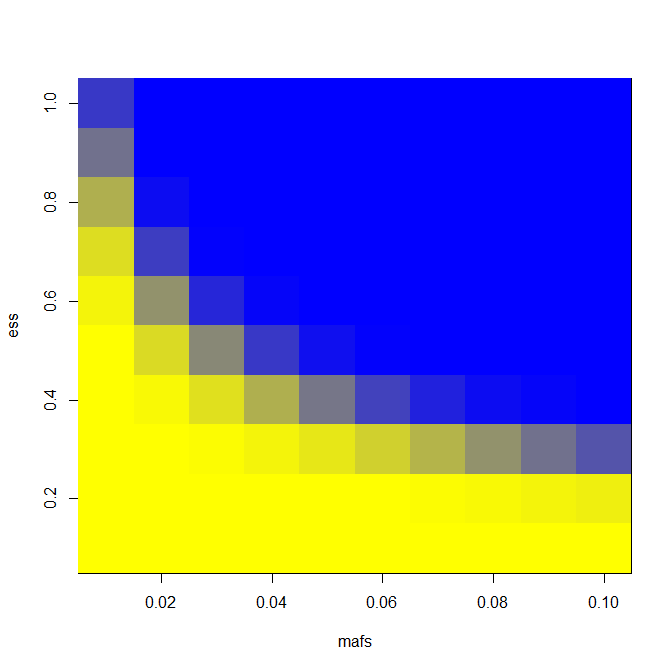
To create the “heat map” that I wanted, I wrote this code to test a range of effect sizes from .1 to 1 standard deviation and minor allele frequencies from 1% to 10%. To be conservative, I assume all unrelated individuals; in reality we’ll have some sibships as well and that will increase power somewhat.
# parameters to run simulation
mafs = seq(.01,.1,.01) # minor allele frequencies to test
ess = seq(.1,1,.1) # effect sizes to test
N = 6000
dprime = .8
alpha = 5e-08 # genome-wide significance
results = matrix(nrow=length(ess)*length(mafs),ncol = 3) # initialize matrix to hold results
counter = 0
for (es in ess) {
for (maf in mafs) {
counter = counter + 1
vq = maf*(es**2) # calculate variance explained
results[counter,] <- c(maf,es,qtl.assoc.power(n=N,vq=vq,p=maf,m1=maf,
dprime=dprime,alpha=alpha))
}
}
colnames(results) = c("MAF","ES","PWR") # name columns
rdf = data.frame(results) # convert result matrix to data frame
library(reshape) # reshape library lets you cast the results into a matrix for visual inspection
temp <- melt.data.frame(rdf,id.vars=c("MAF","ES"),measure.vars=c("PWR")) # melt the data to unique id of (MAF, ES)
cast(temp,ES~MAF,mean) # cast into matrix and display results
k= colorRampPalette(c("yellow","blue"))(100) # generate a yellow-blue color ramp
image(mafs,ess,matrix(rdf$PWR,nrow=length(mafs)),col=k) # plot maf vs. es vs. power
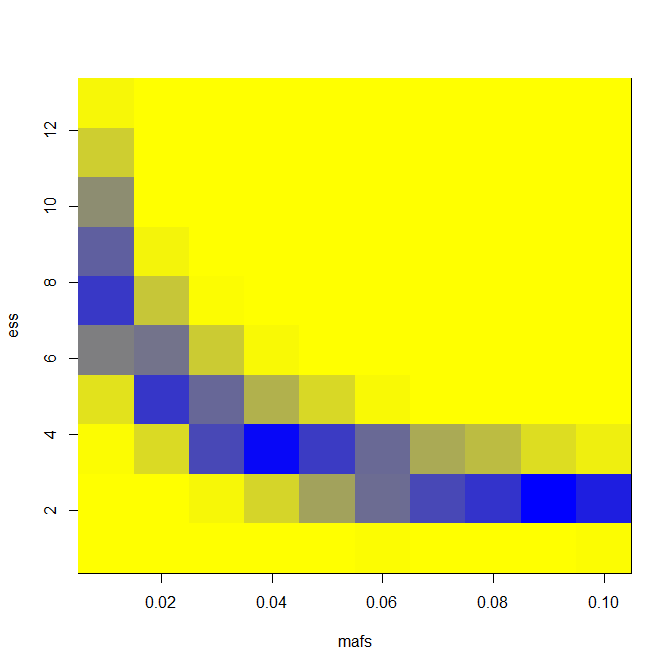
It’s trivial to change the LD assumption; for LD = .8 and N = 6000 as I have above, this is the heat map I get:
With that, I’m halfway there: now I just need to know the power for extreme phenotype sequencing.
Power for extreme phenotype studies
The premier citation for how to calculate power for an extreme phenotype sequencing study is Guey 2011, from Ben Voight’s group at Broad. It presents a simple and powerful simulation approach to calculating power to (1) discover a causal variant, and (2) associate a causal variant with a phenotype, under varying assumptions about MAF, effect size, and how extreme of phenotypes you ascertain from how large a population.
The paper considers “liability”, i.e. an originally-dichotomous phenotype with the phenotypic contribution of known risk factors subtracted to get a continuously varying phenotype that reflects the individual’s supposed genetic liability for the disease. So in that sense it’s a bit different from my study. Whereas I am dealing with a purely quantitative phenotype, Guey still has an underlying affected/unaffected status and so can speak in terms of odds ratios.
Puzzled as to how to adapt this approach to my study, I got in touch with Ben Voight, who very generously spent some time on the phone with me understanding my study and bouncing some ideas back and forth.
The following pseudocode sums up, at a very loose level, my understanding of how the Guey 2011 paper simulates genotype and phenotype. (The way I’m modeling log probability of affected status is probably not exactly right, but you get the general picture):
for all individuals i:
genotype[i] = bernoulli_random_variable(p=freq)
log_probability_of_being_affected[i] = a_priori_disease_prevalence + or_age(age[i]) + or_bmi(bmi[i]) + or_sex(sex[i]) + or_genetic(genotype[i])
phenotype[i] = bernoulli_random_variable(p=exp(log_probability_of_being_affected[i]))
liability[i] = phenotype[i] - age_effect(age[i]) - bmi_effect(bmi[i]) - sex_effect(sex[i])
cases = all i where liability[i] > 98th percentile
controls = all i where liability[i] < 2nd percentile
fisher_exact_test(genotype vs. phenotype, data = controls and cases)
Notice that liabilities are just used for ascertaining extreme cases and controls; the actual association testing uses Fisher’s exact test. The odds ratios they refer to in the paper are the or_genetic term, the amount that the genetic risk factor changes the odds of being affected vs. unaffected. (As opposed to the odds of being extreme case vs. extreme control). And notice that in this simulation, the randomness (unexplained variance in phenotype) is introduced through the fact that the phenotype is decided by a Bernoulli coin flip, where the genetic liability only influences the probability. That corresponds to, in my conception of HD age of onset, the way that I generate an underlying normal distribution and then just spike in the genetic effect.
To adapt this general approach to my residual age of onset quantitative phenotype, I can basically just generate the normally distributed phenotype with spiked genetic effect like I discussed above, then ascertain extreme cases and extreme controls like Guey has done, and simulate doing a Fisher or χ2 test. And because this is sequencing, you don’t need to worry about LD – just assume if the variant is present in your data you’ll find the variant itself.
At Ben’s suggestion I also played with the extra step of modeling effect size in years of life rather than standard deviations. This is a much more intuitive way to discuss effect size. Because this requires working in the space of actual ages of onset rather than log ages of onset, and because I wanted to get away from the assumption of normally distributed residuals anyway, I felt it made the most sense to do this based on sampling (using R’s sample) from my actual data rather than trying to model the distributions of CAG, residuals, etc. none of which are well approximated by canonical distributions (exponential, normal etc).
I actually ran the simulation both ways – with effect size in standard deviations (of residual log age of onset) while assuming normality, or in years of life while sampling without a normality assumption. I’m varying two different things here (the distribution and the way of spiking in genetic effect) so it’s not a good experiment. That said, I don’t think the years of life vs. standard deviations model of effect size makes much of a difference, but I did notice my simulations gave me slightly higher power when I sampled rather than assuming normality. I believe this is because my actual residuals have positive kurtosis, meaning they’re more peaked at the mean than a normal distribution, which means that a spiked-in genetic effect is more “noticeable” as it pushes an individual towards the edge of the distribution.
After all that, here’s my implementation of this simulation in R:
# N = number of individuals for whom to generate genotype and phenotype
# es = effect size. in standard deviations (if how = "normal") or years of life (if how = "sample")
# maf = minor allele frequency of causal snp
# how = how to generate. "normal" = assume residuals are normally distributed. "sample" = sample from actual data stored as global variables
generate.genotype.and.phenotype = function(N,es,maf,how="normal") {
if(how=="normal") { # assume normally distributed residuals; effect size es is in standard deviations
allele_count = rbinom(n=N,size=2,prob=maf)
phenotype = (rnorm(n=N,mean=0,sd=1) + es*allele_count) # normal dist with effect from alleles spiked in
return (data.frame("allele_count"=allele_count,"phenotype"=phenotype))
} else if(how=="sample") { # sample from actual data; effect size es is in years of life
allele_count = rbinom(n=N,size=2,prob=maf)
cag.sim = sample(real.data.cag1,size=N,replace=TRUE) # sample a distribution of CAG lengths
res.log.ao.sim = sample(real.data.res.log.ao,size=N,replace=TRUE) # sample a distribution of residuals
pred.log.ao = model.intercept + model.coefficient*cag.sim # create a predicted log age of onset based on CAG
actual.ao = exp(pred.log.ao+res.log.ao.sim) + es*allele_count # create an actual age of onset based on CAG, residual and genetic effect of causal SNP
# when simulating using actual data sometimes you get a combination of cag and residual where actual age of onset
# ends up being is negative or longer than a normal human life span; identify and exclude these outliers so you
# don't get NA when you take log(actual.ao)
outliers = (actual.ao > 100 | actual.ao < 2) # otherwise in large samples by chance you get negative or too high
actual.ao = actual.ao[!outliers] # clip outliers out of all these vectors
pred.log.ao = pred.log.ao[!outliers]
allele_count = allele_count[!outliers]
res.log.ao = log(actual.ao) - pred.log.ao # create a new residual which includes the genetic effect
phenotype = res.log.ao
return (data.frame("allele_count"=allele_count,"phenotype"=phenotype))
}
}
# maf: minor allele frequency of causal SNP
# es: effect size (meaning depends on "how" parameter below)
# Ntot: number of patients from whom you will ascertain cases and controls
# Nseq: number of people you will actually sequence, in *each* group, so total number sequenced is 2*Nseq
# alpha: already-Bonferroni-corrected threshold at which you want significance, e.g. 5e-08
# niter: number of iterations to use to estimate power
# how: how to simulate phenotype and genotype, "normal" = assume residuals are normally distributed. "sample" = sample from actual data stored as global variables
extreme.phenotype.power.sim = function (maf,es,Ntot,Nseq,alpha,niter,how="normal") {
numsuccess = 0
for (iter in 1:niter) {
sim = generate.genotype.and.phenotype(N=Ntot,es=es,maf=maf,how=how)
phenotype = sim$phenotype
allele_count = sim$allele_count
# ascertain extreme cases and controls
excontrols = (phenotype >= quantile(phenotype,1-Nseq/Ntot)) # top percentiles
excases = (phenotype <= quantile(phenotype,Nseq/Ntot)) # bottom percentiles
# association testing
contingency_table = matrix(c(sum(allele_count[excases]),2*sum(excases)-sum(allele_count[excases]),sum(allele_count[excontrols]),2*sum(excontrols)-sum(allele_count[excontrols])),nrow=2)
f = fisher.test(contingency_table,alternative="two.sided")
p = f$p.value
if (p < alpha) {
numsuccess = numsuccess + 1
}
}
return (numsuccess/niter)
}
# parameters to run simulation
mafs = seq(.01,.1,.01) # minor allele frequencies to test
ess = seq(.1,1,.1) # effect sizes to test
niter = 100
Ntot = 6000
Nseq = 400 # vary this to see effects of choosing larger or smaller number of individuals from same cohort
alpha = 5e-08 # genome-wide significance
results = matrix(nrow=length(ess)*length(mafs),ncol = 3) # initialize matrix to hold results
counter = 0
for (es in ess) {
for (maf in mafs) {
counter = counter + 1
results[counter,] <- c(maf,es,extreme.phenotype.power.sim(maf,es,Ntot,Nseq,alpha,niter,how="normal"))
}
}
colnames(results) = c("MAF","ES","PWR") # name columns
rdf = data.frame(results) # convert result matrix to data frame
library(reshape) # reshape library lets you cast the results into a matrix for visual inspection
temp <- melt.data.frame(rdf,id.vars=c("MAF","ES"),measure.vars=c("PWR")) # melt the data to unique id of (MAF, ES)
cast(temp,ES~MAF,mean) # cast into matrix and display results
k= colorRampPalette(c("yellow","blue"))(100) # generate a yellow-blue color ramp
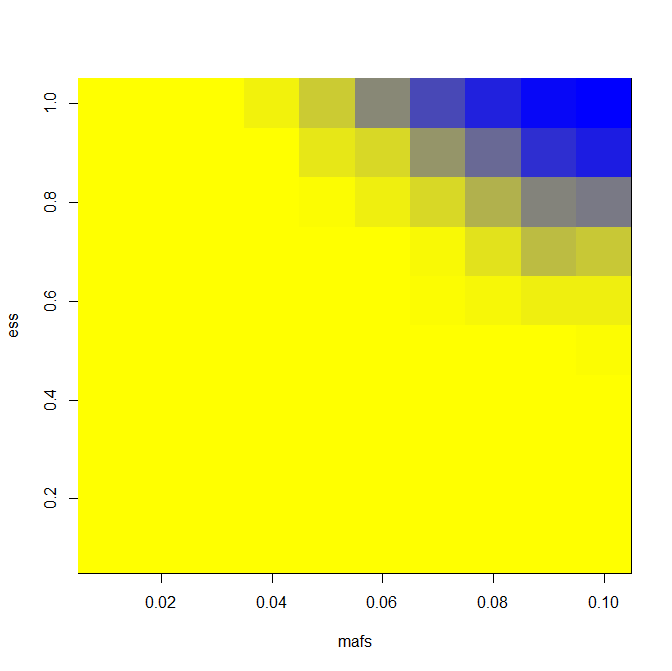
image(mafs,ess,matrix(rdf$PWR,nrow=length(mafs)),col=k) # plot maf vs. es vs. power
And here are results for power when you assume normality and ascertain 25, 100 and 400 cases (and equal number of controls) from a cohort of 6000:
You’ll notice that there’s not that big a gain in power going from 100 to 400 people per group. That’s because we have a fixed cohort size of 6000, so we are getting less extreme of individuals as we expand our sample size. But if you increase the cohort size at the same time as you increase the number of individuals sequenced, you’ll get more and more power.
Comparison of GWAS vs. extreme phenotype exome sequencing
So far I’ve got heat maps of power for GWAS and for extreme phenotype exome sequencing. Now to see the difference in power, I just need to run the two under the same assumptions and subtract the power. If I want to do this with my sampling-and-modeling-effect-size-in-years approach, I need to be able to calculate vq (QTL variance explained) for the given effect size empirically, so I added this function to my quiver:
sample.variance.explained = function(es,maf) {
N = 100000 # large N to calculate variance explained
sim = generate.genotype.and.phenotype(N,es,maf,how="sample")
m = lm(sim$phenotype ~ sim$allele_count)
return (summary(m)$r.squared)
}
With that, I can create a similar heat map where I subtract the two powers to show in what range of MAF and effect size the extreme phenotype study gives a gain in power over the GWAS. Here’s code — this time using sampling and years of effect size, but you can change two lines to how="normal" and es=seq(.1,1,.1) if you want to switch back to “normal” mode.
# compare GWAS power to exphen power
# parameters to run simulation
mafs = seq(.01,.1,.01) # minor allele frequencies to test
ess = seq(1,13,13/10) # effect sizes to test
Ntot = 6000
Nseq = 400
niter = 100
dprime = .5
alpha = 5e-08 # genome-wide significance
results = matrix(nrow=length(ess)*length(mafs),ncol = 3) # initialize matrix to hold results
counter = 0
how = "normal" # what model to assume: normality or sampling from
for (es in ess) {
for (maf in mafs) {
counter = counter + 1
# calculate variance explained
if (how == "normal") { # this is the setting I'm using here
vq = maf*(es**2)
} else if (how == "sample") { # more on this option later
vq = sample.variance.explained(es,maf)
}
gwas = qtl.assoc.power(n=Ntot,vq=vq,p=maf,m1=maf,dprime=dprime,alpha=alpha)
exphen = extreme.phenotype.power.sim(maf,es,Ntot,Nseq,alpha,niter,how="sample")
results[counter,] <- c(maf,es,max(exphen-gwas,0))
}
}
colnames(results) = c("MAF","ES","PWR") # name columns
rdf = data.frame(results) # convert result matrix to data frame
library(reshape) # reshape library lets you cast the results into a matrix for visual inspection
temp <- melt.data.frame(rdf,id.vars=c("MAF","ES"),measure.vars=c("PWR")) # melt the data to unique id of (MAF, ES)
cast(temp,ES~MAF,mean) # cast into matrix and display results
k= colorRampPalette(c("yellow","blue"))(100) # generate a yellow-blue color ramp
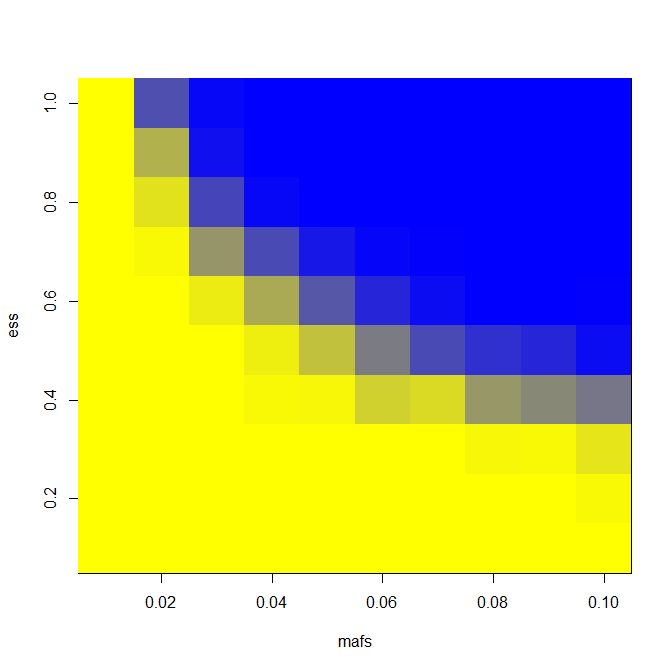
image(mafs,ess,matrix(rdf$PWR,nrow=length(mafs)),col=k) # plot maf vs. es vs. power gained
And here are results for LD = 0.5 and number of exomes sequenced = 400.
You can see an appreciable gain in power for a narrow swath of effect size and MAF combinations. For instance, you’re pretty strongly powered for a 1% MAF SNP with an effect size of 8 years in an extreme phenotype study and not at all in a GWAS, according to this model and these assumptions.
Discussion
All of the simulating and plotting above assumes one causal variant. You could and should ask, what about gene score models? Doesn’t exome sequencing offer extra power not captured by the simulation presented here, through the fact that it allows you to group variants by gene and look for gene-wise association? Yes, it probably does. I have yet to see any papers in the literature that have quantified how much power is gained; if you the reader know of any, please comment on this post! It seems pretty muddled: gene score models that assume unidirectional effect (e.g. RVT1 and RVT2) get diluted if the gene also contains variants with the opposite phenotypic effect; gene score models that allow bidirectional effects (e.g. C-Alpha, SKAT) get diluted if the gene also contains neutral variants. This means that you’ll have even more assumptions to tweak.
One way of thinking about the gain in power from gene score models is that it just lets you group SNPs up to greater frequency. So if you’ve got two causal 1% MAF SNPs, then at best it’s kind of like having one 2% MAF SNP. But by the way, this logic works in GWAS too: if there are two rare causal SNPs in the same gene, then as long as they’re in LD with different marker SNPs or opposite values of the same marker SNP, they’ll both contribute to the height of that association peak on your Manhattan plot.
Personally, I’m not inclined to include any boost in power due to gene score modeling in my power calculation for exome sequencing. Having been through the process once, it seems to me that gene score models will give pretty dramatically different results depending on the model used, the functional filters applied (e.g. including only missense, nonsense, frameshift and splice sites) and the MAF filters applied (most models call for only including variants below a certain MAF, say, 5%). And though I’ve ignored this issue throughout this whole post, exome is exome and GWAS is genome-wide, so this whole comparison assumes that the causal variant is exonic.
You’ll notice that for the final graphic above, I resorted to the rather conservative assumption of LD = 0.5 and I assumed sequencing 400 people per group for a total of 800 exomes. I chose those assumptions for this graphic because under many other sets of assumptions, say, LD = 0.8 and number of exomes sequenced = 100, the extreme phenotype study is actually less powered than the GWAS at every effect size and MAF value.
And that’s where I see the value in this comparison as lying. People are not going to agree on any one set of assumptions — will LD between the hypothetical causal SNP and its nearest marker SNP be 0.8 or 0.5? — but this kind of approach at least lets you see how extreme your assumptions would need to be in order for it to be worth sequencing a given number of exomes. Through that you can hopefully rule out some possibilities, ex. “well we’re definitely not going to bother sequencing just 100 exomes.”
Of course, there is value to having exomes sequenced besides power to associate variants with phenotype, which is all I’ve addressed above. Guey 2011 also explores “power to discover”, i.e. to even happen upon one individual with a given variant and thus know it exists and could be a genetic modifier. If you read the paper you’ll see that power to discover was much higher than power to associate. That could be useful if, say, you want to be able to look under linkage peaks you already know are associated with phenotype, and try to figure out which variant in that region is actually causal. update 2012-12-06: An important point of the Guey’s paper is that power-to-associate is generally pretty low in these sorts of extreme sequencing studies, so the key to getting value out of your study is figuring out how to transfer the information from sequencing to a larger sample. One way is to use sequencing to identify candidate genes for followup genotyping; another way is to use imputation. (Thanks to Ben Voight for clarifying these points!)
Just as with the assumptions regarding LD and so on, reasonable people will disagree about the value of “power to discover” versus “power to associate.” But at a minimum, power calculations should be part of the discussion, and this approach can serve as a decision support tool.
update 2012-12-07: Thinking about this more and looking at Shaun Purcell’s code, it occurred to me that GWAS power depends on absolute linkage disequilibrium (D), not normalized linkage disequilibrium (D’) (see LD definition on Wikipedia). That means you get greatly reduced power if your causal SNP and marker SNP are of different frequencies. All my calculations above assume equal frequencies. How much of a difference does it make? A lot – I ran a little “experiment” assuming a normally distributed phenotype, an effect size of one standard deviation, and a causal SNP MAF of 1%, varying the marker SNP MAF between 1%, 2%, 5%, and 10%. Look at what a difference it makes:
> es = 1 # standard deviations > maf = .01 > vq = maf*(es**2) > qtl.assoc.power(n=6000,vq=vq,p=maf,m1=maf,dprime=.8,alpha=5e-08) [1] 0.7749992 > qtl.assoc.power(n=6000,vq=vq,p=maf,m1=.02,dprime=.8,alpha=5e-08) [1] 0.1382406 > qtl.assoc.power(n=6000,vq=vq,p=maf,m1=.05,dprime=.8,alpha=5e-08) [1] 0.003111842 > qtl.assoc.power(n=6000,vq=vq,p=maf,m1=.10,dprime=.8,alpha=5e-08) [1] 0.0001700689
When you consider that most SNPs on a SNP array used for GWAS will be relatively common (unless you’re using the exome chip), this all means that the gain in power from exome sequencing as opposed to GWAS will be much larger for rare variants than I’ve given it credit for in the brief analysis above. When doing an actual analysis to inform a decision about what study to devote time and money to, it would probably pay to first get a sense of the range of MAFs represented on the chip you’re using in GWAS, and then ask questions about power for rare variants based on that knowledge. end update