Sampling a matching distribution for bootstrapping
Sometimes you just don’t trust statistical tests, and you want an ‘empirical’ p-value to tell you whether your data differ from the null distribution. In those cases it is common to use bootstrapping. This usually takes the following form:
- Randomly generate fake data
- Compare it to your actual data
- Repeat steps 1-2 1000 times. If the real data is ____er than the fake data 998 times out of 1000, then it’s significantly ____ at the p = 2/1000 = .002 significance threshold.
The _____ could be any property you’re interested in testing. A good recent example is Nicolae 2011, who wanted to know whether SNPs that are GWAS hits are more likely to be eQTLs - in other words, whether trait-associated genetic variants are more likely to control gene expression. More likely than what, you ask? More likely than the average SNP that gets genotyped on the SNP chips used for genome-wide association studies. To test his hypothesis, Nicolae generated 1000 random sets of SNPs from the master set of all SNPs included on two popular SNP chips used in GWAS. In Nicolae’s case, the actual GWAS hits indeed contained more known eQTLs than almost any random set of SNPs did (though curiously, the empirical p value is never actually stated).
What makes generating the random sets of SNPs tricky is that sometimes the control SNPs are statistically different from the test SNPs in a confounding way. In Nicolae’s case, the problem is that the GWAS SNPs tend to have higher minor allele frequency (MAF) than random SNPs, because it is easier to detect trait association for more common SNPs.
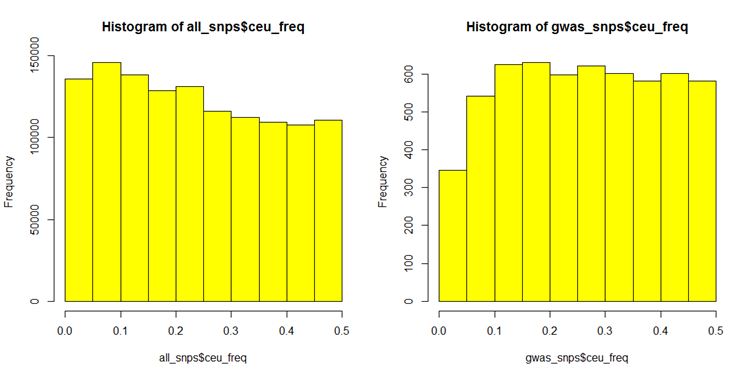
Here are histograms I created based on CEU allele frequencies from HapMap Phase 3 for GWAS catalog SNPs (as of Jan 16, 2013) vs. all SNPs included in the HapMap SNP chips:
Pretty different distributions, huh? That’s a problem for the analysis because if GWAS SNPs have higher MAF, and eQTLs also have higher MAF, then you’ll find enrichment of eQTLs in GWAS whether or not it’s the case that many trait-associated SNPs control traits by controlling gene expression.
To handle this problem, Nicolae drew random sets of SNPs matching on MAF. Specifically, he binned all of the SNPs by increments of 0.05, so there are the 0.00 – 0.05 MAF SNPs, the 0.05 – 0.10 MAF SNPs, etc. Then he drew the same number from each bin in the random sets as were present in the true GWAS set.
I discovered that this binning approach is delightfully easy to implement in PostgreSQL using subqueries to group things into bins and row number() over (partition by... to get just the number of SNPs you want in each bin. This code to create one permutation runs in just 6 seconds:
select sub.snpid
from (
select snpid, floor(p.ceu_freq*20)/20 floorbin, row_number() over (partition by floor(p.ceu_freq*20)/20 order by random()) rn
from platform_snps
) sub, (
select floor(p.ceu_freq*20)/20 floorbin, count(*) n
from platform_snps p, gwas_match gm
where p.snpid=gm.snpid
group by 1
order by 1
) gfc -- gfc = "gwas floorbin counts"
where sub.floorbin = gfc.floorbin -- match on floorbin
and rn <= gfc.n -- limit to number of GWAS hits in that floorbin
;
Note that every time you run this query it will draw with replacement, so some SNPs will appear in more than one permutation. And indeed, you have no choice but to draw with replacement, because there aren’t enough matching control SNPs to let you run 1000 iterations without replacement. You can easily check that using this query:
select control.floorbin, control.n::numeric / gfc.n::numeric max_sets_without_replacement
from (
select floor(p.ceu_freq*20)/20 floorbin, count(*) n
from platform_snps p
group by 1
order by 1
) control, (
select floor(p.ceu_freq*20)/20 floorbin, count(*) n
from platform_snps p, gwas_match gm
where p.snpid=gm.snpid
group by 1
order by 1
) gfc -- gfc = "gwas floorbin counts"
where control.floorbin = gfc.floorbin -- match on floorbin
group by 1,2
order by 1,2
;
For the GWAS catalog (version downloaded January 16, 2013) vs. the platform SNPs from HapMap Phase 3, you could only run at most 136 permutations without replacement before you’d run out of unique SNPs in at least one bin.
Anyway, this binning approach is quick and elegant but it’s a coarse tool. If the underlying MAF distributions are quite different (which they indeed are), then their distribution even within each bin will be different enough that the overall MAF distribution for GWAS SNPs and random SNP sets may prove slightly (but significantly) different. You could get around that problem by going to smaller bin sizes, but when your bins get too small, your whole permutation procedure becomes a house of cards – there is too little variety in which SNPs are selected between the different permutations, and so what appears to be the result of 1000 permutations actually depends heavily on a few sets of SNPs that are represented over and over.
One alternative to binning is to select a particular control SNP for each and every GWAS SNP. In my case, I am interested in matching on LD block size rather than minor allele frequency, but the principle is the same. Instead of counting the number of SNPs with LD block size between 10kb and 20kb and demanding an equal number of control SNPs in that bin, I can demand that each individual GWAS SNP be matched by an individual control SNP whose LD block size is within ±2kb of it.
I couldn’t think of a good way to do this directly in PostgreSQL. Joining every GWAS SNP to every control SNP within ±2kb in block size takes 20 minutes and results in 630 million rows – that’s a lot of effort just to then take one random control SNP for each GWAS SNP. To do this properly you don’t need a full join, you just need to start joining and then give up as soon as you find a single match. PostgreSQL doesn’t provide a way to do that, so I fell back on R. Here’s what I came up with:
library(RPostgreSQL) # first load package RPostgreSQL
drv = dbDriver("PostgreSQL")
con = dbConnect(drv, dbname="enrep", user="postgres", password="postgres", port=5433)
# get list of GWAS SNPs
readsql = "select ld.snpid, ld.blocksize
from ldblocks ld
where exists (select null from gwas_match gm where gm.snpid = ld.snpid)
and ld.blocksize > 1
order by 1
;"
rs = dbSendQuery(con,readsql)
gsnps = fetch(rs,n=-1)
ngsnps = dim(gsnps)[1] # number of GWAS SNPs to match
# get list of available control SNPs
readsql = "select ld.snpid, ld.blocksize
from ldblocks ld
where ld.blocksize > 1
order by 1
;"
rs = dbSendQuery(con,readsql)
csnps = fetch(rs,n=-1)
ncsnps = dim(csnps)[1] # number of control SNPs available for matching
# set up a table to hold permutation results
writesql = "drop table if exists permutations;
create table permutations (
rowid serial primary key,
perm integer,
gsnpid integer,
csnpid integer
);"
rs = dbSendQuery(con,writesql)
set.seed(.1234) # set random seed so results are reproducible
nperm = 2 # for testing - in practice this would be 1000
for (perm in 1:nperm) {
csnps_random = csnps[sample(ncsnps,ncsnps,replace=FALSE),] # draw the control SNPs into a random order
for (i in 1:ngsnps) { # loop through GWAS SNPs to find a match for each
for (j in 1:ncsnps) { # for each GWAS SNP, loop through control SNPs looking for a match
if (abs(csnps_random$blocksize[j] - gsnps$blocksize[i]) < 2000) { # match if blocksize is within 2kb
break
}
}
# then use this SNP in this permutation
writesql = paste("insert into permutations (perm,gsnpid,csnpid) values (",perm,",",gsnps$snpid[i],",",csnps_random$snpid[j],");",sep="")
rs = dbSendQuery(con,writesql)
# and remove it so we don't use it again
csnps_random = csnps_random[-j,]
}
}
dbDisconnect(con)
dbUnloadDriver(drv)
Between the nested loop and the ridiculous number of round-trips to the database, this takes about 5 minutes per permutation (compared to 6 seconds for the binning approach). If I eliminate the repeated insert queries and just save the permutation results to a local vector in the R workspace (to later write to a text file that can be copied into PostgreSQL), then I can can cut that down to about 2.5 minutes per permutation.
While this doesn’t quite rise to the level of incomputable (you could still generate 1000 permutations in a few days of CPU time), it would certainly change the way I do things. With 6 seconds per permutation it has proven very convenient to run everything locally and to just re-create the permuted sets every time I change my mind about the permutation procedure or SNP inclusion criteria. At 2.5 minutes per permutation I’d have to figure out how to parallelize this while keeping the results distinct yet reproducible (setting different seeds for each core?), and the high start-up cost to change anything will make the project less flexible.
So I’m still pondering whether there is a way to do this sort of individual matching more efficiently.
Another issue is what to do when your test and control datasets differ on more than one dimension. The GWAS SNPs and control SNPs differ in MAF distribution, in LD block size distribution, in how likely they are to be protein-coding, and surely in several other ways as well. It seems very difficult to make the permuted distributions match the test distribution on more than one dimension. Instead, I’m planning to match on just one dimension (LD block size) and then try to control for the other things as variables in my model. But if anyone has a better idea, by all means, leave a comment to let me know.
update 2013-01-29: True to form, @a wrote me with a genius algorithm suggestion for generating permutations more quickly:
maybe you want to start by sorting csnps by blocksize. Then for each gsnp, do a binary search to find the lower and upper bounds in the csnps array (at blocksize +/-2k) . Then choose randomly between those two bounds. Should be plenty fast after you finish the initial sort which you only do once.
Sorting the csnps table is trivially fast and can be done in the SQL query to grab the data in the first place. Once it’s sorted, the binary search that @a refers to can be achieved in ~1 second using R’s findInterval function and adding 0.5 to the ranges to make them include ties on both sides:
bottoms = findInterval(gsnps$blocksize-2000.5,csnps$blocksize)+1 tops = findInterval(gsnps$blocksize+2000.5,csnps$blocksize)
Now bottoms is a vector of length ngsnps, which for every gsnp gives you the lowest index into csnps where the blocksize is within -2kb. tops gives you the highest index into csnps where the blocksize is within +2kb.
Then, for each permutation all you have to do is generate a random index using runif. Add 0.5 on each side of the index range so that round gives equal probability to every index in the range:
randomindex = round(runif(n=1,min=bottoms[i]-0.5,max=tops[i]+0.5))
Those three lines of code are basically the entire concept. Below is the new R code. This generates 1000 permutations in just over 1 minute. Amazing. Thanks @a!
library(RPostgreSQL) # first load package RPostgreSQL
drv = dbDriver("PostgreSQL")
con = dbConnect(drv, dbname="enrep", user="postgres", password="postgres", port=5433)
# get list of GWAS SNPs
readsql = "select ld.snpid, ld.blocksize
from ldblocks ld
where exists (select null from gwas_match gm where gm.snpid = ld.snpid)
and ld.blocksize > 1
order by 1
;"
rs = dbSendQuery(con,readsql)
gsnps = fetch(rs,n=-1)
ngsnps = dim(gsnps)[1] # number of GWAS SNPs to match
# get list of available control SNPs, sorted by blocksize
readsql = "select ld.snpid, ld.blocksize
from ldblocks ld
where ld.blocksize > 1
order by 2 asc -- order by blocksize
;"
rs = dbSendQuery(con,readsql)
csnps = fetch(rs,n=-1)
ncsnps = dim(csnps)[1] # number of control SNPs available for matching
# for each gsnp, find lowest index in sorted csnps array that has blocksize within -2kb
# because all block sizes are integers, adding 0.5 to ranges makes ranges inclusive of all ties
bottoms = findInterval(gsnps$blocksize-2000.5,csnps$blocksize)+1
# for each gsnp, find highest index in sorted csnps array that has blocksize within +2kb
tops = findInterval(gsnps$blocksize+2000.5,csnps$blocksize)
set.seed(.1234) # set random seed so results are reproducible
nperm = 1001 # for testing - in practice this would be 1000
totalrows = ngsnps*nperm # total rows in output table
# set up columns for final match table matching gwas snps to their permutation matches
permno = vector(mode="integer",length=totalrows)
gwassnpid = vector(mode="integer",length=totalrows)
permsnpid = vector(mode="integer",length=totalrows)
# first 'permutation' is just the GWAS SNPs themselves - this is convenient for my analysis
for (i in 1:ngsnps) {
permno[i] = 1
gwassnpid[i] = gsnps$snpid[i]
permsnpid[i] = gsnps$snpid[i]
}
# latter permutations are randomly drawn from the control SNPs
for (perm in 2:nperm) { # start from permutation #2 since GWAS SNPs are perm #1
for (i in 1:ngsnps) { # go through every GWAS SNP index
rowno = (perm-1)*ngsnps+i # calculate master row index for final table columns
randomindex = round(runif(n=1,min=bottoms[i]-0.5,max=tops[i]+0.5)) # randomly choose an index within bounds
permno[rowno] = perm # permutation number
gwassnpid[rowno] = gsnps$snpid[i] # snpid of GWAS SNP being matched
permsnpid[rowno] = csnps$snpid[randomindex] # snpid of permuted SNP
}
}
# write results to disk
finaltable = data.frame(permno,gwassnpid,permsnpid)
write.table(finaltable,'c:/sci/019enrep/data/rperms-2013-01-29.txt',sep='\t',append=FALSE,col.names=FALSE,row.names=FALSE)
# call PostgreSQL to read the results back from disk.
sql = "drop table if exists rpermutations;
create table rpermutations (
perm integer,
gwassnpid integer,
permsnpid integer
);
copy rpermutations from 'c:/sci/019enrep/data/rperms-2013-01-29.txt';"
rs = dbSendQuery(con,sql)
dbDisconnect(con)
dbUnloadDriver(drv)