How to calculate heritability
Heritability is the proportion of variance in a particular trait, in a particular population, that is due to genetic factors, as opposed to environmental influences or stochastic variation.
That’s just a general definition to give you a feel for it. Actually we need to be more rigorous than that. There are two definitions of heritability. A common simplification in all sorts of genetic studies and models is to assume that all alleles and all genotypes act independently of each other – this is called an ‘additive model.’ So for instance, if one allele of a particular SNP gives you a 1 cm increase in height, then being homozygous for that SNP should give you a 2 cm increase in height. Clearly, this model doesn’t allow for dominant or recessive effects, even though we know these abound. It also doesn’t allow for gene-gene interactions, where maybe that SNP only gives you a 1 cm increase in height if paired with another SNP. For these reasons, the additive model is a huge simplification, but a useful one. Now for the two definitions of heritability:
- ‘narrow sense heritability’ (h2) is defined as the proportion of trait variance that is due to additive genetic factors
- ‘broad sense heritability’ (H2) is defined as the proportion of trait variance that is due to all genetic factors including dominance and gene-gene interactions.
Both kinds of heritability are incredibly tricky to estimate and to interpret. In terms of estimation, a big problem is that people who share parts of their genome tend to share parts of their environment too. One simple way you might think to estimate heritability is to plot children’s traits against the average of their parents, as shown in this example from Visscher 2008: 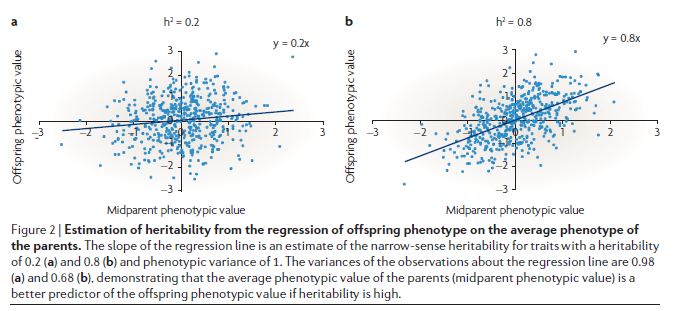
In the example above, the slope is taken to be the heritability. The problem with this is that parent and child share a lot else besides half their genome.
One approach to calculating heritability which largely avoids the confounding of genotype with shared environment is to compare the phenotypic concordance of monozygotic (MZ, identical) twins versus dizygotic (DZ, fraternal) twins. Both types of twins are expected to share virtually all environmental factors, including while in the womb, which is why this is a better study design than just comparing MZ twins to siblings. Comparing MZ to DZ twins lets you isolate the contribution of that marginal half shared genome to phenotypic concordance.
Visscher 2008, citing Deary 2006 (ft), discusses the example of IQ, where MZ twins have concordance of .86 and DZ twins have concordance of .60. ”Concordance” in these studies seems to refer to a Pearson’s correlation or similar, so something like an r or ρ. (Why r and not slope, like in parent-offspring regression? See this post for further discussion).
At first glance it is not clear how to convert these numbers – .86 and .60 – into an estimate of heritability. After all, both of these figures include both genetic and environmental factors. The key observation is that sharing a marginal half genome with your twin explains an additional .86-.60 = 26%, so in theory, sharing a full genome explains 2*26% = 52%.
This is called Falconer’s formula:
heritability = 2(rMZ - rDZ)
I wrote “heritabiliity” on the left side of the equation, instead of h2 or H2, because it is debatable what this estimate is really reflecting. The wiki on Falconer’s formula claims that it estimates H2, broad-sense heritability. Indeed: since MZ twins share virtually all their genotypes (there will be just a few chance mutations here and there that make them differ), they share dominant / recessive effects and gene-gene interactions, which DZ twins are not expected to share. Yet the notion that you can just double the 26% marginal variance explained by a half genome in order to extrapolate to a whole genome seems to assume all additive effects. The 26% marginal variance explained from sharing a whole genome as opposed to a half genome might in fact be partitioned between additive effects (which we could fairly double to extrapolate to a whole genome), gene-gene interactions (which we should perhaps multiply by 4/3, since DZ twins sharing half their genome only share 1/4 of their possible gene-gene pairings, so the MZ twins are capturing an extra 3/4) and dominance effects (which we might also argue to multiply by 4/3 since DZ twins share both alleles at only 25% of sites, so again, MZ twins add a marginal 3/4).
Accordingly, though the wiki on Falconer’s formula claims it calculates H2, the wiki on twin studies claims it estimates h2. To my view, it’s not a perfect estimate of either of these. And frustratingly, grand sweeping reviews of the concept of heritability (such as Visscher 2008) are long on talk and short on formulae.
I also ran across an old school paper by Jacquard 1983 (ft) which presents a formula something like this:
heritability = (ρMZ - ρDZ)/(1-ρDZ)
So for the IQ example, heritability = (.86-.60)/(1-.60) = .26/.40 = 65%. This will often give pretty different answers than Falconer’s formula; I don’t quite understand the logic of it, though one nice property of it is that it never rises above 100%. But I can’t find any evidence that this alternative formulation is still in use today.
Besides the H2 vs. h2 debate, there are other conceptual issues with calculating heritability from twin studies as well. For instance, MZ twins may actually share more environmental factors than DZ twins since being similar makes people treat them similarly. It’s entirely possible to find that ρMZ - ρDZ > 50%, in which case your estimate of heritability will be > 100%. Oops. Also, it is assumed that DZ twins share exactly half their genome, but in fact, due to random segregation of alleles, there is variance in what fraction of alleles siblings actually share – more on this shortly.
There are plenty of other study designs as well. Whereas MZ vs. DZ twin studies look at the effect of sharing 100% IBD instead of ~50%, sibling vs. adopted sibling studies look at the effect of ~50% IBD instead of 0% IBD, while theoretically controlling for shared environment (though obviously it can’t account for factors in the womb). Here, h2 = 2(ρsib - ρadoptee) (*The Falconer’s Formula wiki says not to double this quantity, i.e. h2 = ρsib - ρadoptee – this seems incorrect to me, but if you know otherwise, please leave me a note)
Twin pairs and sibling/adoptee pairs are all well and good when you’re dealing with a trait like height, which you can measure for absolutely anyone. But consider the phenotype of residual age of onset in Huntington’s Disease. This phenotype can only be assessed for people who have HD, which is already a very rare disease; if you were to also limit yourself to twin pairs you’d have an n pretty close to zero. In that case, you’ll take what you can get, such as correlation between sibling pairs: 2*rsib is an upper limit for heritability. It might be a pretty loose upper bound, and if rsib > 50%, then it’s no upper bound at all. If you have other relationships in your dataset as well – parent-offspring pairs, avuncular pairs, cousin pairs – then you can try to make a few more inferences, though it is pretty hard to disentangle genes and environment because unlike in the MZ/DZ and sibling/adoptee comparisons you don’t have any pairs of pairs where environment is shared equally between the two pairs but genotype is shared unequally. In U.S.–Venezuela Collaborative Research Project 2004, the most oft-cited study of heritability in HD age of onset, the siblings had concordance of .42 (suggesting an upper bound for heritability of 84%) while parent-offspring were only .10, avuncular .07 and cousin .15 [see Table 4]. Under an additive model (narrow-sense heritability), the parent-offspring correlation would suggest heritability of no more than 2*.10 = 20%, the avuncular would suggest 4*.07 = 28%, and the cousins no upper limit at all because 8*.15 > 100%. In short, the data are all over the place. The authors assumed that only siblings share an environment, and then used some model (details never stated; see my commentary here) to integrate all these pieces of information into a single estimate of 38% heritability. This should probably be interpreted as a pretty rough estimate.
Here’s a thought exercise: suppose the Venezuelan HD pedigree has some consanguinity, which means that relatives often share more IBD than their nominal relations to each other would suggest. Does that bias the heritability estimate? I am still undecided on my answer. At first I thought the answer was no, because if you think of heritability as (variance explained by genes) / (total variance), then both the numerator and denominator are affected by consanguinity. Yes, first degree relatives share ‘extra’ IBD and so correlate better than they ‘should’, but so does everyone in that dataset. However, Visscher 2006 presents formulas for controlling for parent inbreeding, implying consanguinity does matter. Leave me a comment if you have the answer.
In talking about consanguinity, my concern is with excess IBD. But you might also ask whether excess identity-by-state (IBS) matters for heritability calculations. After all, even if you only look at SNPs that are polymorphic within my ethnic group, I’m still going to share plenty of alleles with any other random person just by chance. For a C/T SNP with minor allele frequency 50%, there are three possible genotypes CC, CT and TT, and so me and some random person will have a 50% chance (.25^2 + .5^2 + .25^2) of sharing a genotype and a 87.5% chance of sharing at least one allele (1-2*.25^2). And most SNPs are relatively uncommon, with an average minor allele frequency around 10 – 15% in many studies, which makes those odds even higher. Accordingly I’ll also share way more than half my alleles with my sibling just by chance. So does that mess up the heritability calculations? Again, since it affects both the numerator and denominator – you have extra IBS with your siblings and with random people in the population – I believe the answer should be no.
However, leaving consanguinity behind now, the fact is that different sibling pairs do share different amounts of IBD, and different unrelated individuals do share different amounts of IBS. This variability has enabled a couple of very cool modern approaches to calculating heritability.
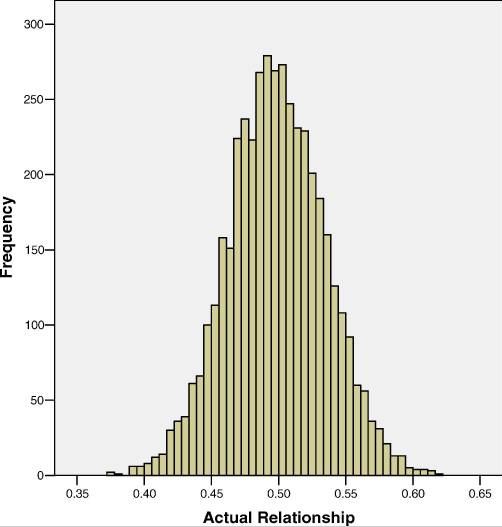
The first of these is sibling IBD regression. Visscher 2006 presents an excellent (and perhaps the first with any considerable sample size?) analysis of heritability of height using this approach. Due to random segregation of parental alleles, siblings don’t always share exactly 50% of alleles IBD. The mean is 50%, standard deviation ± 4% – a fair number of sibling pairs share as little as 40% of alleles or as many as 60%, as shown in Visscher’s histogram from Figure 1:
The fact that some siblings are more similar to each other than other pairs are – yet we assume they all have an equal degree of shared environment – gives us a new way to estimate heritability, while controlling for environment, without having twins available. That’s pretty cool! Visscher’s formulas are under Materials and Methods; there is a lot of fancy stuff you’ll need to know to implement it and estimate standard error, correct for inbreeding if present, etc., but the core concept is just to regress siblings’ genotypic concordance (% shared IBD) against their phenotypic concordance. This is done as follows (these formulas assume exactly 2 sibs per family):
- Let Yi1 be the (quantitative) phenotype of sibling 1 in family i
- Let πi be the percent IBD between siblings 1 and 2 in family i
- Let σ̂p2 be the estimate of total phenotypic variance in the population
- α and β are parameters to be estimated
- ĥ2 will be your estimate of the additive genetic (narrow sense) heritability
Then:
- Use this formula to estimate β: (Yi1-Yi2)2 = α + βπi
- Then plug your estimated β̂ into this formula: ĥ2 = β̂/(2σ̂p2)
The Achilles heel of this approach, as Visscher points out, is that the standard errors are really high. That’s because the range of sibling IBD is relatively narrow (not many sib pairs outside the .4 to .6 range). Visscher’s simulations suggest that when the true h2 is 0.8 and the sample size is 2500 sib pairs, the standard error of h2 is 0.2. That gives you a pretty wide range, but I’d point out that different studies give widely differing estimates of heritability anyway, at least for some traits (for instance Visscher 2008 cites IQ heritability estimates ranging from 0.5 to 0.8). Estimating heritability, even in the best of circumstances, is not an exact science. Visscher’s estimate of height heritability obtained via sibling IBD regression is 0.8, which is consistent with the estimates obtained by other methods.
If you can exploit the variation in IBD among siblings to estimate heritability, why not exploit the variation in IBS among unrelated members of the general population? Even nominally unrelated individuals will vary in how many alleles they happen to share, and you can measure this using SNP chip genotyping data. For any trait believed to have complex genetic etiology – many loci each contributing small effects – more genotype sharing should mean greater phenotypic concordance. This, to my understanding, is the principle behind Visscher’s latest tool, GCTA [Yang 2011]. It’s offered as a Unix command line tool that you can run out of the box with PLINK pedigree files haplotyped using MaCH. I don’t fully understand all the math yet – I’ll post an update if I get my head around it – but I believe the basic principle is regressing unrelated individuals’ genotypic concordance against phenotypic concordance. Because unrelated individuals don’t share a household environment, you again have a sort of ‘control’ that lets you begin to separate out the effects of environment vs. genetics. Admittedly, it gets messy if you consider that some genotypes correlate with some environmental factors, etc. – e.g. SNPs that predispose you to smoking, which you of course inherited from your parents, mean you’re more likely to have grown up with second-hand smoke in the house. A couple of caveats are that (1) this only works well for common variations, since rare variations are less well tagged by SNPs on your SNP chip, and (2) because the level of genotypic concordance among unrelateds is so much smaller and less variable than between siblings, the standard errors are even higher than for sibling IBD regression. So you need huge sample sizes. Still, this is pretty cool stuff.
But: don’t be fooled by all this fancy math into thinking that the genetics field is super advanced and sophisticated on precisely calculating heritability. There are a ton of issues with how to interpret heritability estimates. Visscher 2008 does a good job of addressing these. One important point is that heritability depends on the estimate of phenotypic variance in a particular population at a particular moment in time. Americans today are both taller and more obese than their ancestors 100 years ago, even though (at a population level, within ethnic groups, and to a first approximation, etc. etc.) their genes haven’t changed. We think height is about 80% heritable [Visscher 2008], but that’s just under today’s conditions – if you compared height across the whole of human history, you would be adding a ton of additional non-genetic variance, and the proportion explained by genetics – the heritability – would accordingly shrink. So just because a trait is highly heritable doesn’t mean it’s genetically deterministic.
A gross estimate of heritability also tells you nothing about the architecture of heritability. A trait that is 80% heritable could be caused by one locus that explains 80% of variance, or 80 loci that each explain 1% of variance. So just because a trait is highly heritable doesn’t mean there will be any individual genetic variants of large effect size.
An additional challenge in interpreting heritability estimates is that economic incentives bias which figures get reported. For any given trait, there will be a range of different estimates of heritability in the literature – say 0.5 to 0.8 – and even within any one study, there will probably be a range of possible estimates depending on the exact methodology chosen. In general, the highest estimate will be the one that researchers prefer to cite, because high heritability means justification for grant applications to fund GWAS and sequencing projects to identify the genes that drive heritability. So part of the ‘missing heritability’ probably lies in the fact that, for a huge range of human traits, the estimates of heritability that we hear most often are a bit, well, optimistic.