How censoring by life expectancy affects age of onset distributions
In late-onset genetic diseases, reported ages of onset are almost always based on observed cases – i.e. individuals who did have onset of disease. For instance, reported ages of onset for genetic prion diseases [Kong 2003] are simply based on published case reports of individuals affected by these diseases.
There are several problems with determining age of onset distributions from observed symptomatic individuals. It ignores the information that could be gleaned from asymptomatic individuals who are still alive and well at the time the study was published. It ignores any bias towards diagnosis and ascertainment of severe or early onset individuals – and this is particularly severe when published case reports are used as the source of data, since more remarkable cases are more likely to be published. It also ignores the fact that some people will die of other causes before experiencing onset of the genetic disease they carry.
There is no such thing as a 100% penetrant late-onset disease. No matter how lethal a disease is at age 50, the fact is that several percent of people never live to see their 50th birthday anyway. This is old hat to actuaries, who will surely find the analysis in this post laughably oversimplified. However, here in the world of bioinformatics, genetic epidemiology, and genetic counseling, there seems to be relatively little awareness of the way that life expectancy affects age of onset estimates. The purpose of this post is therefore to explore how the “censoring” of individuals who die of other causes, based on the life expectancy distribution, affects age of onset estimates in genetic diseases.
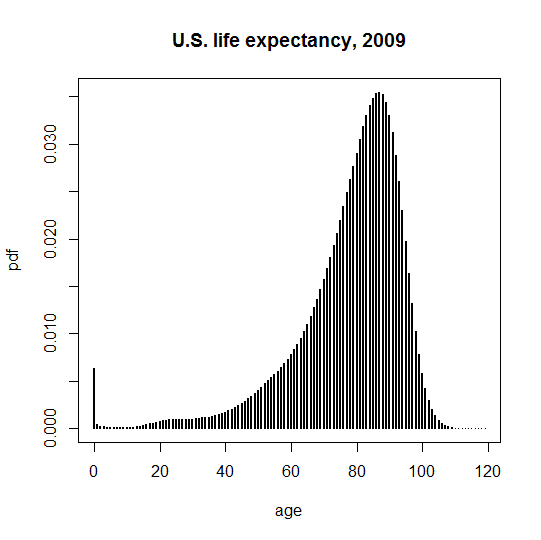
My dataset for this analysis is the U.S. Social Security Administration’s 2009 Actuarial Life Table. Here is a plain text, analysis-ready version of it: [ssa.actuarial.table.2009]. Combining men and women, here is a probability density function (PDF) of when people die, viewed prospectively from age 0:
# actuarial life table
# http://www.ssa.gov/oact/STATS/table4c6.html
life = read.table('ssa.actuarial.table.2009.txt',sep='\t',header=TRUE)
life$age = as.integer(life$age)
life$msur = as.numeric(life$msur)
life$fsur = as.numeric(life$fsur)
# calculate percent surviving. this is 1-CDF.
life$mpctsur = life$msur/100000
life$fpctsur = life$fsur/100000
life$allpctsur = (life$msur + life$fsur) / 200000
# calculate probability, from age 0, of dying at each possible age. this is the PDF.
life$pdf = life$allpctsur - c(life$allpctsur[-1],0)
plot(life$age,life$pdf,type='h',lwd=2,xlab='age',ylab='pdf',main='U.S. life expectancy, 2009')
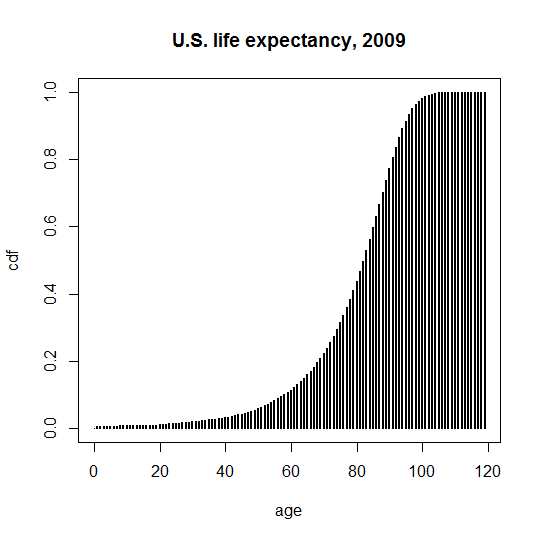
A different way to view this is with the cumulative distbution function (CDF), i.e. the faction of people that have died by a certain age:
plot(life$age,1-life$allpctsur,type='h',lwd=2,xlab='age',ylab='cdf',main='U.S. life expectancy, 2009')
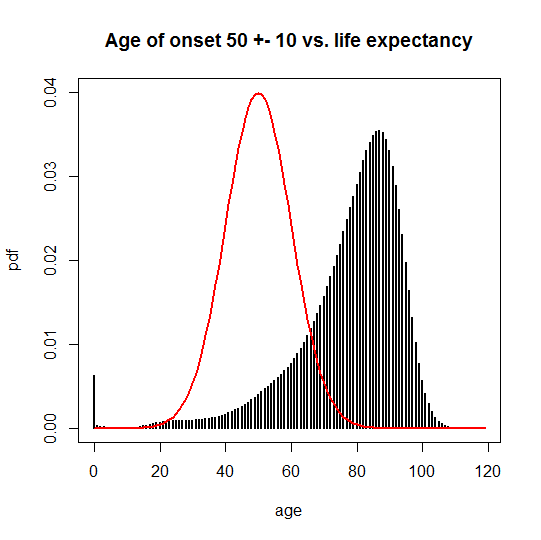
The later the age of onset for a genetic disease, the more it will overlap with these curves. In other words, the later the age of onset, the more people will already be dying of other causes by the time the genetic disease comes to get them. The way to assess this formally is to integrate over the CDF of the disease age of onset distribution times the PDF of the life expectancy distribution (thanks @Learner). In R, the p___ functions give the CDF, so pnorm is the CDF of a normal distribution. For a hypothetical genetic disease with a normally distributed true age of onset of 50 ± 10, the penetrance is given by:
sum(pnorm(0:119,m=50,sd=10)*life$pdf)
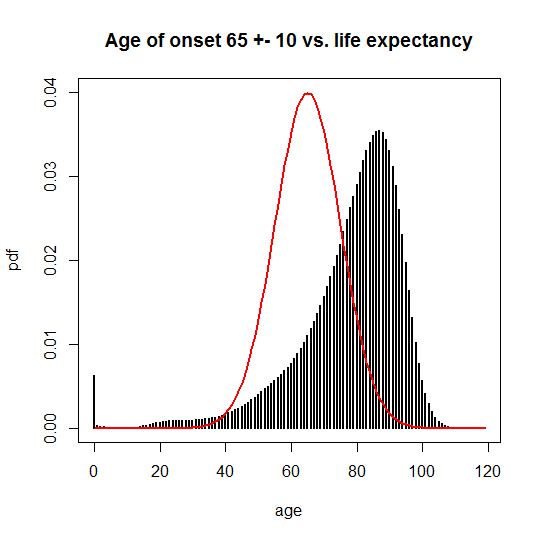
= 92.3%. Whereas for a disease with an age of onset 65 ± 10,
sum(pnorm(0:119,m=65,sd=10)*life$pdf)
= 79.5%. Remember, these figures are just the penetrance according to how many people die of something else before they die of the disease – I’m still assuming that the disease really is fully penetrant as long as you live long enough to die of it.
For me, at least, the easiest way to visualize the censoring of observed individuals is to plot the age of onset PDF over the life expectancy PDF. For the disease with mean onset at age 50:
And for 65 ± 10, you can see there’s much more overlap:
This overlap has two consequences. One is that neither disease has complete penetrance, and the N(65,10) disease has a lower penetrance than the N(50,10) disease. Another is that the age of onset one would compute based on only the observable cases (people who didn’t die of something else first) is different from the true onset. You can calculate the observable average age of onset as an average weighted by the probability of people still being alive at each possible age of death:
sum((0:119)*dnorm(0:119,m=50,sd=10)*life$allpctsur)/sum(dnorm(0:119,m=50,sd=10)*life$allpctsur)
sum((0:119)*dnorm(0:119,m=65,sd=10)*life$allpctsur)/sum(dnorm(0:119,m=65,sd=10)*life$allpctsur)
So the N(50,10) disease will appear to have an age of onset of 49.5, and the N(65,10) disease will appear to have an age of onset of 63.5. Those figures aren’t so different – indeed, well within the margin of error for most diseases for a million other reasons. But the older the true age of onset and the wider the variance on the true age of onset, the bigger the difference between that and the observed age of onset.
I set out to try every combination of “true” mean from 40 to 80 with “true” standard deviation from 5 to 10 years, censor it with the life expectancy distribution and see how it changes. Then when I read about a disease with a given observed age of onset distribution, I can look it up in this table and see what the true age of onset distribution might be. I wanted to also get out skewness, kurtosis and median – stuff that I couldn’t figure out how to derive from first principles, so I did it as a simulation instead, with 100,000 men and 100,000 women:
nr = length(40:80)*length(5:15) # number of rows in output table
translate = data.frame(TRUEMEAN=numeric(nr),TRUESD=numeric(nr),TRUEMEDIAN=numeric(nr),OBSMEAN=numeric(nr),OBSSD=numeric(nr),OBSMEDIAN=numeric(nr),OBSSKEW=numeric(nr),OBSKURT=numeric(nr),OBSPCTF=numeric(nr),PENETRANCE=numeric(nr))
i = 1 # row counter
for (truemean in 40:80) {
for (truesd in 5:15) {
sex = c(rep('M',100000),rep('F',100000))
true.onset = round(rnorm(m=truemean,sd=truesd,n=200000))
p.penetrant.m = life$mpctsur[match(true.onset[sex=='M'],life$age)] # probability of penetrance (i.e. not dying of something else first) for each man
p.penetrant.f = life$fpctsur[match(true.onset[sex=='F'],life$age)] # and each woman
p.penetrant = c(p.penetrant.m,p.penetrant.f) # concatenate together
p.penetrant[is.na(p.penetrant)]=0 # as a consequence of assuming a normal dist of onset, you sometimes get onset outside of 0:120 range, resulting in NA. convert these to 0.
observed.mean = weighted.mean(true.onset,w=p.penetrant,na.rm=TRUE)
# weighted variance: http://stackoverflow.com/questions/10049402/calculating-weighted-mean-and-standard-deviation
normalized.weights = p.penetrant / sum(p.penetrant)
observed.var = sum(normalized.weights * (true.onset-observed.mean)^2)
translate$TRUEMEAN[i] = truemean
translate$TRUESD[i] = truesd
translate$TRUEMEDIAN[i] = median(true.onset)
translate$OBSMEAN[i] = observed.mean
translate$OBSSD[i] = sqrt(observed.var)
# sketchy way i made up to calculate weighted median:
is.penetrant = runif(min=0,max=1,n=100000) < p.penetrant # booleans for whether a person is penetrant, based on p.penetrant
translate$OBSMEDIAN[i] = median(true.onset[is.penetrant])
translate$PENETRANCE[i] = sum(p.penetrant)/200000
translate$OBSSKEW[i] = skewness(true.onset[is.penetrant])
translate$OBSKURT[i] = kurtosis(true.onset[is.penetrant])
translate$OBSPCTF[i] = sum(p.penetrant.f,na.rm=TRUE)/(sum(p.penetrant.f,na.rm=TRUE)+sum(p.penetrant.m,na.rm=TRUE)) # percent of disease sufferers who are female
i = i + 1
}
}
# also make observed mean & sd rounded to nearest integer, to make lookups easier.
translate$ROBSMEAN=round(translate$OBSMEAN)
translate$ROBSSD=round(translate$OBSSD)
write.table(translate,'true.vs.observed.ao.distributions.txt',row.names=FALSE,col.names=TRUE,quote=FALSE)
That code takes about 1 minute to run. Results are here: [true.vs_.observed.ao_.distributions.txt]. A few observations: the higher the true age of onset mean and/or the higher the true standard deviation:
- …the larger the difference between true and observed mean, and sd.
- …the larger the percent of female patients.
- …the larger the negative skew and negative kurtosis in the observed distribution
- …the lower the penetrance.
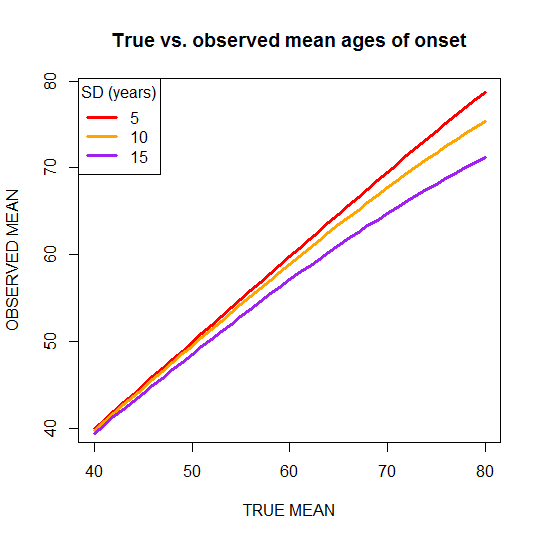
Here’s a plot of true vs. observed mean ages of onset for three different levels of standard deviation:
plot(translate$TRUEMEAN[translate$TRUESD==5],translate$OBSMEAN[translate$TRUESD==5],type='l',lwd=3,col='red',xlab='TRUE MEAN',ylab='OBSERVED MEAN',main='True vs. observed mean ages of onset')
points(translate$TRUEMEAN[translate$TRUESD==10],translate$OBSMEAN[translate$TRUESD==10],type='l',lwd=3,col='orange')
points(translate$TRUEMEAN[translate$TRUESD==15],translate$OBSMEAN[translate$TRUESD==15],type='l',lwd=3,col='purple')
legend('topleft',c('5','10','15'),pch='-',lwd=3,col=c('red','orange','purple'),title='SD (years)')
You can see that for low ages of onset, the true and observed mean are always pretty close under the assumptions used here. For instance, for fatal familial insomnia, the reported mean age of onset of 49 [Kong 2003 , Gambetti 2003 (ft)] may not be too far off the mark, at least not for reasons of censoring due to deaths by other causes. On the other hand, consider E200K Creutzfeldt-Jakob Disease, with a reported mean age ofonset around 63 +- 11 [Schelzke 2012]:
> translate[translate$ROBSMEAN==63 & translate$ROBSSD==11,] TRUEMEAN TRUESD TRUEMEDIAN OBSMEAN OBSSD OBSMEDIAN OBSSKEW OBSKURT OBSPCTF PENETRANCE ROBSMEAN ROBSSD 283 65 12 65 62.57622 10.97664 63 -0.1677716 -0.07780673 0.5250138 0.7853813 63 11 294 66 12 66 63.40562 10.90435 64 -0.1627119 -0.07709475 0.5258163 0.7715524 63 11
If the true distribution is normal, then the true mean is probably more like 65 or 66, and the observed penetrance is ~77%. Censoring by life expectancy could well contribute to explaining why the observed penetrance of the mutation is incomplete [Goldfarb 1991]. A thorough analysis using actuarial life tables concluded that, just as in my simulation here, the penetrance is complete as long as you don’t die of something else first [Spudich 1995 (ft)].
But this is all a pretty simplistic analysis. There’s no reason to assume that the “true” age of onset distribution for any disease must be normal. Throw in some kurtosis or skewness, and the answers to the above analysis will change quite a bit. And people dying of other causes is by no means the only reason for incomplete ascertainment. Young, severe cases are more likely to come to the attention of the medical establishment, more likely to be reported in literature. People with family history are more likely to be diagnosed correctly. And when families are considered, there are also a variety of sources of bias towards including earlier-onset children and later-onset parents – see [Penrose 1948 (ft)] for the foundational work in that area. Also consider that, where life tables are concerned, a lower life expectancy (for instance, in developing countries or in the U.S. in decades past) will give a lower observed mean age of onset.
The above-cited work on E200K [Spudich 1995 (ft)] is one of the few papers I’ve seen in the prion literature that gives a fairly systematic treatment of the possible biases. Likewise in Huntington’s Disease, many studies examining the relationship between CAG repeat length and age at onset simply analyze patients who have already become symptomatic and/or passed away [Ranen 1995 (ft), Maat-Kievit 2002, USVCRP 2004, Andresen 2007]. Not surprisingly, some of the most robust analyses of Huntington’s, taking into account age-dependent penetrance, life tables, ascertainment, etc., have come out of the actuarial world [Gutierrez & MacDonald 2002, Gutierrez & MacDonald 2004], but there have also been good analyses by the genetics people too [Brinkman 1997 (ft), Langbehn 2004]. Also of note, there has been some modeling of the likelihood of having a family history vs. being the first symptomatic individual in the family, based on CAG expansion frequencies, in [Falush 2001].
An excellent review and meta-analysis of all the HD CAG / age of onset models, along with the only prospective analysis in the literature, can be had in [Langbehn 2010]. Not surprisingly, Langbehn’s Figure 1 shows that for low CAG lengths (36-42) where penetrance is incomplete, the Langbehn and Gutierrez & MacDonald models that account for censoring give much higher estimates of the true mean age of onset than do the purely observational models. Langbehn also raises an important related issue: for genetic counseling purposes, the relevant figure is not the global mean age of onset, but the conditional expected age of onset based on the patient’s current age. The older you are, the later your expected age of onset, since you’ve already dodged the particularly early bullets. Of course, this is true of life and death in general, not just genetic diseases – the SSA 2009 tables show that, for instance, although life expectancy for women in the U.S. at birth is 80, once you’re 79 you still have an additional 10 years to live on average – not just 1.
Indeed, the biases inherent in estimating age of onset for genetic diseases – failure to account for censoring, the use of absolute rather than conditional life expectancy, the possibly higher diagnosis and reporting rate for young and severe cases – all seem to push towards the reported mean ages of onset being at least slight underestimates. It’s tough to model the extent of this underestimation (note again how overly simplistic the analysis in this post) without prospective / longitudinal data. But it’s still important to keep in mind. It’s also good news.