Last week, shopping around for a night school class, I went to introductory lectures on organic chemistry and biochemistry and was introduced, again, to the concept of chirality, which I’ve never understood.  The idea is that for an atom bonded to four different R groups, there are two different orderings of the R groups.  This should be simple enough and there are plenty of good tutorials on it online, including this Khan Academy lecture:

But I must just have poor 3-D spatial reasoning skills.   I simply couldn’t wrap my mind around how the two “orderings” of atoms in 3-D space could be fundamentally different.

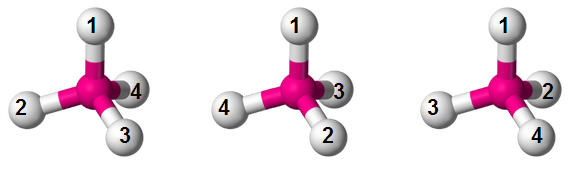
After all,  I figured, there is only one way to arrange three keys on a keychain.  Although there are 3! = 6 orderings of keys, rotation makes 3 of them identical and flipping the keychain over makes 2 of them identical, thus 3!/3/2 = 1.  I illustrate this using my flashlight, Hubway RFID keyfob, and one actual key.  Here are three rotations:

keys.rotated.side1

And by flipping it over and rotating again, here are the other three permutations:

keys.rotated.side2

A chiral atom has four R groups, not three, but it also gets to move in 3 dimensions, not just 2.  I just couldn’t picture what it means for the 4 R groups to have fundamentally different orderings.  So I tried rotating a molecule 120° at a time, sort of like I was rotating the keys.

chirality.rotated.1

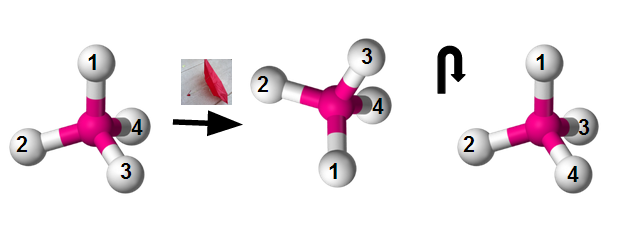
And I got three rotations, but sure enough, you just can’t get the 2-4-3 ordering with the 1 on top through any rotation in three dimensions.  Instead, I realized, the equivalent of flipping the keychain would be to flip the molecule inside out like Boston windstorms have done to so many umbrellas:

umbrella.inside.out

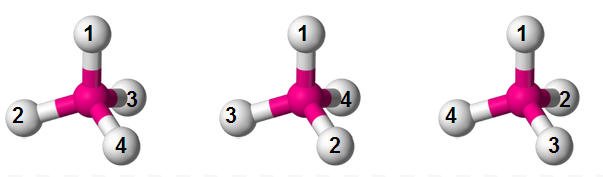
By which I mean, pointing the 2, 3, and 4 prongs of the tetrahedron upward and having the 1 stick out the bottom.  If you do this to the original molecule and then rotate it around again, you can indeed get the 2-4-3 configuration:

chirality.insideout.rotate

And then if you rotate this, you do indeed get all three other rotations of the 2, 3 and 4:

chirality.rotated.2

The catch, of course, is that the umbrella-like inversion of the molecule is not just a rotation in 3-D space.  Flipping it inside out makes it a different molecule – the enantiomer of the original molecule.  In fact, this act of turning a chiral molecule inside out is precisely what happens in SN2 reactions (see also SN1, E1 and E2).

So to go back to the key analogy, having the 1 anchored at the top is equivalent to if you considered your keychain to have “sidedness”, in which case there would indeed be chirality to your keychain.

My next question was why I’ve heard people say that everything in biology has the same chirality.  Isn’t it totally arbitrary which version of a molecule we call which?  In what meaningful sense are biomolecules of the same chirality?

In the following sense: in all of the 20 (or 21 or 22) canonical, genetically encoded amino acids, the R group is in the same position relative to the COO-, NH3+ and H groups.  This particular configuration happens to be L, meaning it rotates light counterclockwise.   Biological sugars, on the other hand, are D and rotate light clockwise.

A molecules’ D or L light-rotating properties are difficult to predict and have often been determined experimentally.  Without knowing whether a molecule is D or L, there is still a convention called the Cahn-Ingold-Prelog priority rules for calling a molecule R or S based on the ordering of the molecular weights of the attached groups.

Chirality was discovered by Louis Pasteur examining crystals of tartaric acid in wine.  A crystal seed of one chirality will only precipitate from solution molecules of its same chirality, so you can end up with macroscopic crystals of all one chirality.

PS. Given that I had trouble visualizing this 3-D phenomenon, imagine how flummoxed I was by Adam Bliss’s stereographic projections of a hypercube!

Special thanks: Emily Ricq helped me finally understand this material.