In a post last month I presented a simple exponential model of prion propagation in vivo and then tested whether it could explain the relationship between PrPC expression level and prion incubation time. The answer: it couldn’t, at least not without a little help. One way to force it to fit the data was to suppose that PrPC available for conversion is limited by some other factor (e.g. space in lipid rafts) and that overexpressing PrPC saturates this limited resource.

In this post I’ll show that the relationship between PrPC expression and incubation time isn’t all that’s hard to explain in a simple exponential model.  It turns out to also be quite hard to reconcile this model with the relationship between incubation time and the inoculated dose of prions.

the model

Recall from last time that the basic model we’re talking about here is:

T(t) = T_0 e^{(k_{conversion}S_0 - k_{degradation})t}

Where T(t) is the amount of PrPSc or infectivity (which I’m still treating interchangeably for now), T0 is the starting titer of prions, kconversion is a constant describing how quickly PrPSc can convert PrPC S0 is the PrPC expression level, kdegradation is a constant describing the degradation of PrPSc, and t is time. In this post, S0 or PrPC expression is not my primary concern, so I’ll simplify by defining a constant φ:

\varphi = k_{conversion}S_0 - k_{degradation}

So that:

T(t) = T_0 e^{\varphi t}

A curious fact about prion kinetics is that the prion infectivity titer by the time of onset of symptoms seems to be about the same regardless of PrPC expression level and regardless of the titer of the original inoculum. It’s tough to say for sure because there’s so much experimental variability, but certainly if you look at the titers at time of onset in the mice across several different PrPC expression levels in a few different papers [Bueler 1994, Fischer 1996, Sandberg 2011], it is difficult to make a case for the values being significantly different. As for titer of inoculum, my assumption is that an animal inoculated with a low dose that gets sick after a long time and an animal inoculated with a high dose that gets sick after a short time have about the same amount of infectivity in their brains at the time they each get sick. I haven’t managed to find as good of citations for this assumption, so please comment if you know.

In any case, for now I’m going to assume that the titer at time of onset is invariant, a quantity I’ll call Tonset. Tonset appears to correspond to about 109 ID50 units in the entire brain of a Sc237-infected hamsters according to [Prusiner 1982a]. I think it’s about the same in RML-infected mice: Bueler 1993 finds titers of ~8.1-8.6 log10 ID50s per mL in a 10% dilution. That implies >9 log10 ID50/mL in pure brain homogenate, and a mouse brain is about half a gram and therefore its volume is probably something like half an mL. We’re in the right ballpark at least.

So if we assume that Tonset is a constant, we’ll say 109, then the model above lets us solve for the relationship between the incubation time or tonset and the inoculum titer T0:

T_{onset} = T_0 e^{\varphi t_{onset}}
ln(T_0) = ln(T_{onset}) - \varphi t_{onset}

In fact, as I mentioned in the last post, titer is lost rapidly in the first few days of prion infection, then recovers over the following weeks, so the inoculum or T0 is not quite the right value to start from. But let’s return to that later and just observe that the above model implies that:

t_{onset} \propto ln(T_0)

Where ∝ means “is linearly proportional to”. The model suggests that the incubation time is proportional to the log of the inoculated titer.

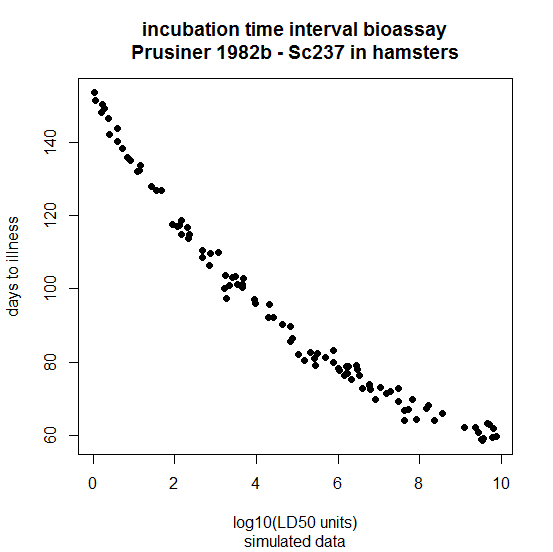
That’s not what has been observed in reality. 30+ years ago, Prusiner sped up the study of prions by pioneering the use of incubation time bioassay (instead of endpoint titration) to determine prion titers [Prusiner 1982b]. The raw data aren’t given in the paper, but I’ll simulate them by adding some random noise to the model he got out of the data:

logdose = runif(n=100,min=0,max=10) # simulate 100 different experiments with diff titers
days = 10^( (logdose-26.66)/(-12.99) ) + 40 + rnorm(n=100,m=0,s=2) # apply Prusiner's model
plot(logdose,days,xlab="log10(LD50 units)",ylab="days to illness",pch=19,
     main="incubation time interval bioassay\nPrusiner 1982b - Sc237 in hamsters",
     sub="simulated data")

The model he derived from regression on his data was essentially this:

log(titer) = 26.66 - 12.99(log(t_{onset}) - 40)

Note that it implies two things. First, you can never have an incubation time under 40 days, no matter how high the titer. Second, instead of the log-linear relationship above, it implies a log-log relationship:

log(t_{onset}) \propto -log(T_0)

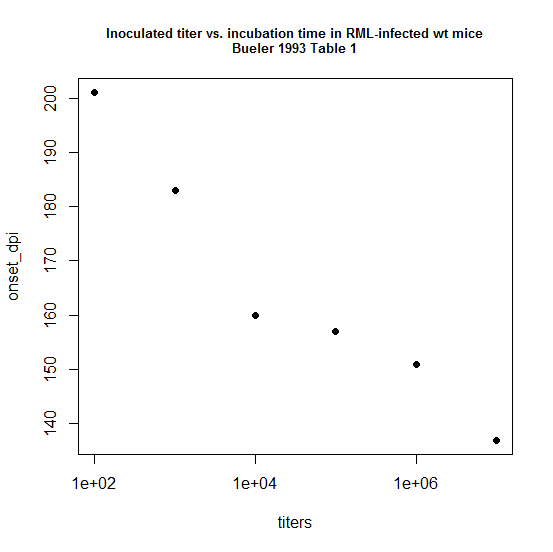
That paper was on the Sc237 strain in hamsters. I couldn’t found the equivalent model for RML in mice, so I took a look at the data in Table 1 of Bueler 1993. The “disease” row of the “inoculum” column shows times to clinical disease for animals inoculated with dilutions from 10-1 to 10-7, though not all the 10-7 animals got sick, so they’re not useful for modeling. The text of the paper states that the 10-1 dilution contained about 107 ID50s total (in 30μL), implying the source had a titer of 108 (again, ID50 per 30 μL. Note this implies 109 ID50 per 300μL, so probably on the order of 109 ID50 per brain).

I’ll throw these data points into a quick plot:

# RML based on Bueler 1993 Table 1
source_titer = (1e7)*10 
onset_dpi = c(137,151,157,160,183,201) # Table 1 "inoculum" column, "disease" row
dilutions = 10^-(1:6)
titers = source_titer * dilutions
plot(titers,onset_dpi,log='x',pch=19,cex.main=.8,
     main='Inoculated titer vs. incubation time in RML-infected wt mice\nBueler 1993 Table 1')

Even with just 6 data points, the relationship is clearly there. First I’ll try a log-linear model, one where:

t_{onset} \propto -log(T_0)

logtiter = log10(titers)
m = lm(logtiter ~ onset_dpi)
summary(m)
#Coefficients:
#            Estimate Std. Error t value Pr(>|t|)    
#(Intercept) 17.34296    1.73838   9.977 0.000567 ***
#onset_dpi   -0.07791    0.01046  -7.449 0.001735 ** 
#Multiple R-squared:  0.9328,    Adjusted R-squared:  0.9159

The model has some explanatory power (adjusted R^2 = .9159) and the relationship is clearly significant. What if I try a log-log model?

m = lm(logtiter ~ log10(onset_dpi))
summary(m)

It’s even better, with an adjusted R^2 of .9357. This must have been what Prusiner first observed when developing the incubation time bioassay. What he found was that the R^2 was maximized when you took the log not of the incubation time itself, but of the incubation time minus a constant – in his case, 40 days. Let’s find out what the best constant is to fit the Bueler RML data:

find_best_adjustment = function(onset_dpi, titers) {
    # try every possible "adjustment" up to the lowest incubation time observed
    days_to_test = 1:(min(onset_dpi)-1)
    rsq_vals = numeric(length(days_to_test))
    for (dpi_adjustment in days_to_test) { 
        log_adjusted_dpi = log10(onset_dpi - dpi_adjustment)
        m = lm(logtiter ~ log_adjusted_dpi)
        rsq_vals[dpi_adjustment] = summary(m)$adj.r.squared
    }
    # figure out which model had the highest R^2
    return ( which(rsq_vals == max(rsq_vals)) )
}

find_best_adjustment(onset_dpi, titers)
# 100

The answer: 100 days. With this adjustment in place, we get an adjusted R^2 of .9492:

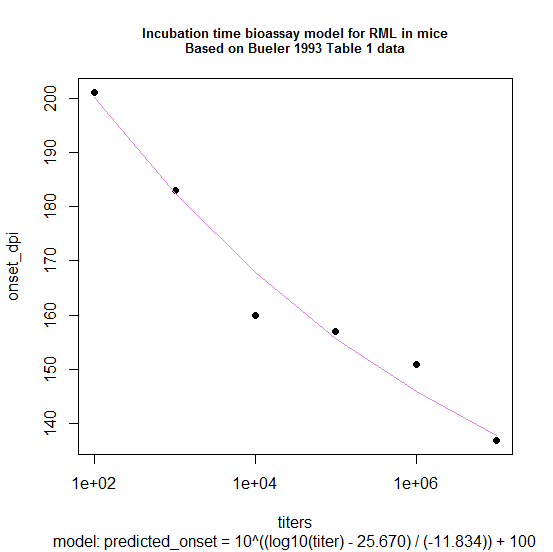
dpi_adjustment = 100
log_adjusted_dpi = log10(onset_dpi - dpi_adjustment)
m = lm(logtiter ~ log_adjusted_dpi)
summary(m)
#Coefficients:
#                 Estimate Std. Error t value Pr(>|t|)    
#(Intercept)        25.670      2.185   11.75 0.000300 ***
#log_adjusted_dpi  -11.834      1.218   -9.72 0.000627 ***
#Multiple R-squared:  0.9594,    Adjusted R-squared:  0.9492

The model can be used in either direction:to predict incubation time given a titer, or to estimate titer given an observed incubation time:

estimated\_titer = 10^{25.670 - 11.834*log10(onset\_dpi - 100)}
predicted\_onset = 10^{(log10(titer) - 25.670) / (-11.834)} + 100

Here’s how it fits the data:

predicted_onset = function(titer) {
    return ( 10^((log10(titer) - 25.670) / (-11.834)) + 100 )
}
plot(titers,onset_dpi,log='x',pch=19,cex.main=.8,
     main='Incubation time bioassay model for RML in mice\nBased on Bueler 1993 Table 1 data',
     sub='model: predicted_onset = 10^((log10(titer) - 25.670) / (-11.834)) + 100')
points(titers, predicted_onset(titers), type='l', col='violet')

It’s interesting that even with a pitiable amount of data (just 6 points) I can already see the same result reported in [Prusiner 1982b]: that a log-log model, with some “adjustment” to the days-to-onset figure, fits better than a log-linear model.

That’s bad news for our simple exponential model, which really wants the relationship to be log-linear. But we know that model was doomed to be way too simple, so I wanted to see if it was possible to rescue it by accounting for one thing I haven’t accounted for so far: the fact that the inoculated infectivity is very rapidly degraded.

I discussed this at the beginning of the last kinetics post, so see that for background. Basically, the data from Bueler 1993 imply that inoculated infectivity is degraded with a half-life of ~5h – much faster than half-lives reported for PrPSc later on in disease. Why is that? It could be that exogenous (extracellular) PrPSc is degraded much more quickly than endogenous (membrane-bound) PrPSc. But another explanation that tempts me is the idea that PrPC is a limiting reactant in those first few days after inoculation. This would appear to explain why sometimes there is barely any difference at all in incubation times for the few highest titers (for instance, in Fischer 1996 Table 2, the 10-1 and 10-2 dilutions both give 69-day incubation times). Once you’ve saturated the available PrPC, there’s nothing left to do.

So I set out to see whether accounting for this might save the model and explain why a log-log relationship is observed empirically. The right way to do this would be a complicated system of differential equations where inoculum is degraded rapidly while converting new endogenous PrPSc which concurrently begins to convert other PrPC molecules. After fiddling with that for a bit, I decided perhaps it was wiser to start with something a bit simpler. So I split my model into two phases: 1) a phase where exogenous PrPSc is degraded at a rate described by constant ψ while it also converts endogenous molecules, and 2) a phase where those nascent endogenous PrPSc molecules now propagate at a rate described by constant φ, which I introduced earlier. In this model, I define Tmin to be the minimum titer reached after, let’s say, 4 days, when the exogenous PrPSc is basically gone but the endogenous PrPSc hasn’t begun multiplying yet. We’ll return to phase 1 in a moment; first observe that what’s going to happen in Phase 2 is this:

T_{onset} = T_{min} e^{\varphi (t_{onset} - t_{min})}

And so what our equation for Phase 1 needs to tell us is the value of Tmin – how much endogenous PrP has the inoculum managed to convert in its first 4 days before it’s gone forever? What I’m probing is the idea of PrPC being limiting, so I’m going to make a slightly non-intuitive use of the Michaelis-Menten equation, which states:

v = \frac{v_{max}[S]}{K_m + [S]}

Where v is the reaction velocity, vmax is its maximum possible value in the presence of unlimited substrate, Km is a constant describing affinity for substrate and [S] is the concentration of substrate. This equation does a great job of describing some saturable systems, where a reaction requires both A and B (usually an enzyme and its substrate) and by increasing B without bound you can, only asymptotically, fully utilize A. My non-intuitive use of this involves thinking of v as the number of PrPC molecules converted per unit time, vmax being the sum of available PrPC at any given moment, [S] being the amount of PrPSc i.e. inoculum titer, and Km being, again, a constant to do with affinity. I’ll define the number of endogenous PrPSc molecules as N(t) and the number of exogenous inoculum PrPSc molecules as X(t) (N like eNdogenous, X like eXogenous) and swap in all my favorite variables: v = dN/dt, vmax = S0, and [S] = X(t), so:

\frac{dN}{dt} = \frac{S_0 X(t)}{K_m + X(t)}

Note that the Michaelis-Menten equation normally describes initial velocity of a reaction, before you’ve had time to deplete the substrate; here, I’m treating it as describing the velocity for all time t. That’s because I’m assuming that PrPC is produced constantly in the cell, so its depletion due to conversion to endogenous PrPSc is not an issue; and that exogenous PrPSc is depleted far faster by degradation (modeled in X(t)) than by binding to PrPC. Remember, that degradation is described by a new constant ψ so:

X(t) = X_0 e^{-\psi t}

Because dN/dt depends on X(t) but not on N(t) itself, we can simply plug X(t) in:

\frac{dN}{dt} = \frac{S_0 X_0 e^{-\psi t}}{K_m + X_0 e^{-\psi t}}

Now what I want is an expression for N(t). I spent an hour or so trying to get it by integration by parts, which I’m certain can be done, but it somehow eluded me, so finally I gave in and used integral-calculator.com, which gave this:

N(t) = -\frac{S_0}{\psi}ln(X_0 e^{-\psi t} + K_m)

In fact, what integral-calculator.com does NOT do for you is compute the constant, often denoted C, which you can have in front of any integrated expression due to the fact that it would drop out upon differentiation. So that equation really should be:

N(t) = C - \frac{S_0}{\psi}ln(X_0 e^{-\psi t} + K_m)

In this case, we know that we start with zero endogenous PrPSc molecules, so N(0) = 0, and plugging that in we can get that:

C = \frac{S_0}{\psi}ln(T_0 + K_m)

Putting it together,

N(t) = \frac{S_0}{\psi}ln(T_0 + K_m) - \frac{S_0}{\psi}ln(X_0 e^{-\psi t} + K_m)

With a half-life of only 5 hours, the inoculum will be pretty much gone after a few days, but just to be safe, we can ask how many endogenous molecules it will manage to convert as t trends toward infinity.

\lim_{t \to \infty}N(t) = \frac{S_0}{\psi}ln(T_0 + K_m) - \frac{S_0}{\psi}ln(K_m)

Or, rearranging a bit,

\lim_{t \to \infty}N(t) = \frac{S_0}{\psi}ln(\frac{T_0}{K_m} + 1)

Now remember that the number of endogenous molecules produced by that inoculum before it dies off are the seed for all future prion propagation, the Tmin in the model for Phase 2:

T_{onset} = T_{min} e^{\varphi (t_{onset} - t_{min})}

Observe that (assuming X(t) ≈ 0 at tmin):

T_{min} = \lim_{t \to \infty}N(t) = \frac{S_0}{\psi}ln(\frac{T_0}{K_m} + 1)

We know from the Phase 2 equation that:

t_{onset} \propto -log(T_{min})

And now we can see from the expression for the limit of N(t) that:

T_{min} \propto log(T_0)

Plugging this into the equation for tonset, then, it would appear that:

t_{onset} \propto -log(log(T_0))

Which isn’t what we wanted at all! We started with the problem that the exponential model suggests a log-linear relationship while empirical evidence gives a log-log relationship. Modeling the saturation of PrPC in the first few days of infection didn’t fix that problem, in fact, it made it worse – now we have log(log())-linear relationship.

incubation time bioassay in wild-type versus overexpressing mice

So, this model isn’t looking so good, and I might be about done with it. But I promised in the last post that I would compare the incubation time bioassay curves between wild-type and overexpressing mice, and I want to follow up on that quickly. If I slightly modify my above code to handle the data on Tga20/Tga20 mice (10x expression level) from Fischer 1996 Table 2, I get:

tga20_onset = c(69,69,87,111) # Fischer 1996 Table 2
source_titer = (10^7)*10
dilutions = 10^c(-1,-2,-4,-6)
titers = dilutions*source_titer
logtiter = log10(titers)
m = lm(logtiter ~ tga20_onset)
summary(m) # .9245

find_best_adjustment(tga20_onset, titers)
# 46

m = lm(logtiter ~ log10(tga20_onset - 46))
summary(m) # .9492

So once again, the log-log model works better than the log-linear model – this time with just 4 data points. And the optimal “adjustment” to make to the days-to-onset is 46 days, implying that no matter how high the titer, you just can’t get a quicker incubation than 46 days in RML-infected Tga20/Tga20 mice. Note that, compared to wild-type mice, the incubation time at the 10-1 dilution dropped by about half (137 vs. 69 days) and the theoretical minimum incubation time also dropped by about half (100 days vs. 46 days). (Aside: it appears Fischer didn’t use any “adjustment” at all: “Titers were determined by the incubation time assay (Prusiner et al., 1982), using the relationship y = 14.37-1.1x, where y is log LD50 and x is incubation time (days) to terminal disease.”)

In my last post I used the series of PrPC expression levels in Fischer 1996, to twist my model into saying that the “effective” PrPC expression level in a 10x mouse is actually more like 1.3x. If you plug that into this equation for Phase 1:

\frac{dN}{dt} = \frac{S_0 X(t)}{K_m + X(t)}

You’ve now got S_0 increasing by a factor of 1.3x, so at every moment t, 1.3x as much endogenous PrPSc is being produced, so you end up with Tmin being 1.3x greater. Then, in Phase 2, your prion production is increased in two ways: Tmin is greater by 1.3x, and you also get φ being larger by some unknown amount (φ = kconversionS0 – kdegradation, so it depends on what the k values are). In other words, my two-phase model predicts a yet even larger difference in incubation times between different PrPC expression levels than the simple model from last month did, and even the model from last month predicted too large a difference, leading to this idea of PrPC saturation and the 10x meaning really 1.3x. Long story short, my two-phase model is even more divergent from reality than a one-phase model.

conclusions

My two-phase model didn’t do a good job of explaining the log-log relationship between inoculated dose and incubation time. Nor did it explain the idea of a “theoretical minimum” incubation time of, say, 40 days for Sc237 as implied by [Prusiner 1982b] or 100 days for RML as found above, since log(log()) grows very slowly but does, nevertheless, grow without bound. It is interesting to speculate, then, on why there do appear to be hard limits on how fast an incubation time can be achieved at higher and higher titers. Though my particular model didn’t work out, I don’t rule out the possibility that the idea of saturation could play into it somehow. After all, we need to explain the fact that infectivity actually drops dramatically in the first few days of infection, then is very slow to recover. And there’s a testable hypothesis in here somewhere: if the “minimum” incubation time is a result of how much infectivity can survive those first few days, then multiple inoculations should be able to overcome this and give arbitrarily short incubation times. In particular, the same total titer distributed over multiple inoculations should give a shorter incubation time than if that total was administered in a single large bolus. It is clear that repeated exposure to a limiting dilution of prions increases the incidence of successful infection [e.g. Diringer 1998, Jacquemot 2005] but I am not aware if anyone has formally looked at the relationship between incubation time and how an identical dose is divided between time points.

Others before me have considered simple models for prion kinetics and have rejected them in favor of more complex models based on the linear, fibrillar nature of amyloids, whether made of PrP or other proteins [Masel 1999, Poschel 2003, Tanaka 2006, Knowles 2009]. After all, scrapie fibrils look linear under an electron microscope: they’re clearly fibrils and so it stands to reason they’re infectious only at their two ends. That they must break in order to form new ends and achieve exponential growth is the principle behind PMCA. My next task in the prion kinetics space will be to get more familiar with these models and understand whether they can explain all of the strange phenomena I’ve raised in this post and my last.

P.S. all the above code is available in a single script here.