Exome sequencing reveals disease modifiers for cystic fibrosis
In yesterday’s post on QQ plots, I showed a simulated QQ plot from “the GWAS of your dreams” in which all observed p values clung tightly to expectation (indicating good, unbiased data) except for a few p values that stood far above the curve (indicating you’ve discovered genes or variants that actually matter). Apparently sometimes GWAS dreams do come true:
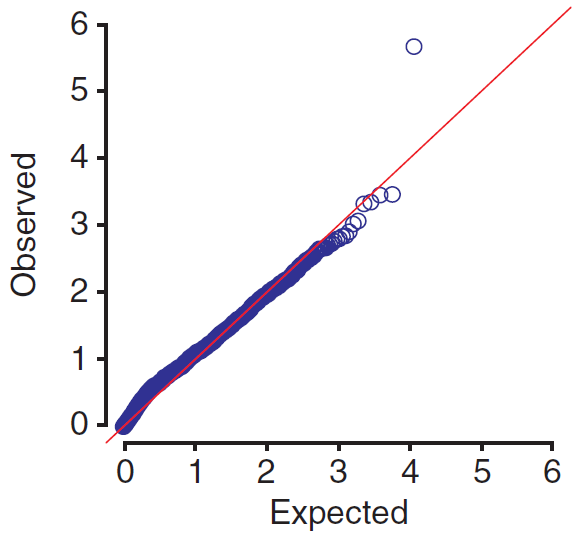
That’s Figure 1a from Emond’s “Exome sequencing of extreme phenotypes identifies DCTN4 as a modifier of chronic Pseudomonas aeruginosa infection in cystic fibrosis”, [supplement] published in Nature Genetics last month. The paper is just as stunning as the graphic in its clarity and conclusiveness. Pseudomonas aeruginosa infection is a major part of the pathophysiology of cystic fibrosis, and Emond discovered that rare variants in DCTN4 are significantly associated with earlier and more chronic infections. The paper is an excellent tour of the methodology needed for this sort of study, so this post will walk through the “how-to”.
In terms of general approach, there are two things really notable about Emond’s approach as distinct from the other GWAS I’ve reviewed on this blog:
- Emond chooses extreme phenotypes (43 early, 48 late onset) to increase statistical power.
- Emond looks specifically at rare variants (for the initial screen, those with minor allele frequency less than 12.5%, though she also re-runs the analysis with other thresholds; Fig 1a is based on a 5% threshold).
Why rare variants? Emond explains this choice in the supplement:
The general thrust of the recent strategies to analyze rare variants is to exclude common variants from the collapsed (by gene) score given to each individual for each gene in an association analysis. The reasons for this are that common variants can usually be tested for association via a SNP chip based GWAS, as long as the sample size and MAF combination are large enough to achieve reasonable power for the test. Common variants are also more likely to have no association with phenotype, and including such variants in the collapsed score would have a detrimental effect on power to detect any association between the phenotype and the rare variants.
Consider also that because common variants are common, in order to detect a causal one in a GWAS you’d need either a large sample size (larger than the 91 people in this study) or the variant would need to have a very large effect size so that it segregates very cleanly between case and control (ex. at this locus, all 43 early patients have C, all 48 late patients have G). Despite what Pasaniuc has to say, a lot of people still think that such common variants are better elucidated through SNP array-based GWAS, while the comparative advantage of exome sequencing in association studies lies in its ability to detect rare variants that don’t make it onto SNP arrays.
Now, when you’re looking at rare variants, you can’t afford to do the analysis at the variant level, because you’d find a whole lot of variants present in 1 case and 0 controls. That’s never going to be significant. But it could be the case that several of your cases each have a different rare variant in the same gene (or same pathway, etc.) leading to the same (or similar) loss of function and the same phenotype. So you group the variants by what Morris and Zeggini 2010 call a “functional unit” – most likely a gene, but a pathway could work too.
When you group by gene, there are a couple of different ways to pose your question: “are cases more likely to have more rare variants in this gene than controls?” or “are cases more likely to have at least one rare variant in this gene than controls?”. These, in essence, are models RVT1 and RVT2 (respectively) as introduced by Morris and Zeggini. These authors run both models on a simulation and find that RVT1, based on “the proportion of rare variants at which an individual carries minor alleles”, is more powerful across the board– even when the phenotype is actually caused by having at least one rare variant, which is the case RVT2 is designed to detect. Therfore “RVT1 is awesome” seems to be the take-home message from Morris and Zeggini’s paper and that’s the method Emond uses. It’s a logistic regression on the proportion of minor alleles to fit a coefficient indicating the effect of that proportion on phenotype. Here is how Morris and Zeggini introduce it:
Consider a sample of unrelated individuals, phenotyped for a normally distributed trait, and typed for rare variants in a gene or small genomic region. Let ni denote the number of rare variants for which theith individual has been successfully genotyped, and let ri denote the number of these variants at which they carry at least one copy of the minor allele. We can model the phenotype, yi, of the ith individual in a linear regression framework, given by yi = E[yi]+ɛi, where ɛi,σE), and
In this expression, xi denotes a vector of covariate measurements for the ith individual, with corresponding regression coefficients β. The parameter λ is the expected increase in the phenotype for an individual carrying a full complement of minor alleles at rare variants compared to an individual carrying none.
That’s basically the model that Emond runs to find DCTN4. Emond found 11,542 genes meeting their criteria: MAF < .125 and “the distribution of variants was not collinear with the risk group variable” (there are two risk categories for cystic fibrosis, so any variants that segregate with the lower or higher risk group would have muddied the results). So that means 11,542 p values from 11,542 regressions, each performed across the 91 individuals in the study. The model is just slightly more complicated than the above, by the inclusion of a couple of other controls: Emond also controlled for risk group, and did a principal component analysis to find three principal components associated with ancestry and control for those as well. After getting the 11,542 p values, Emond applied a Bonferroni correction and found that DCTN4 was the sole significant gene (naive p = 2.2e-6, corrected p = .025).
Inspection of the DCTN4 variants in the samples revealed that there were two different rare variants: of the 43 early onset patients, 9 had a variant at rs11954652 (pretty rare) and 3 had a variant at rs35772018 (very rare and highly conserved).
Next, Emond double-checked this result in just about every way imaginable, and it stood up to every test. It is remarkable how thoroughly this result was validated– both in additional statistical models and in additional patients– before it went to publication. Here are the steps Emond took to validate her finding:
- Re-ran the RVT1 analysis with only variants with MAF < .05
- Ran a SKAT-O test (due to Lee, S 2012; see p.8 and p.25 of the supplement). According to Emond, this test:
uses a variance components approach that can capture genes that have variants at different sites that contributing to different extremes of phenotype. (Such variants will make the overall “burden” in the cases and controls look similar and result in a high p-value for the MZ test, which does not account for the direction of effect.)
- Ran an EREC test (due to Lin & Tang 2011; see p. 9 and p. 25 of the supplement). Like the SKAT-O, this also accounts for genes with multiple variants pushing in opposite phenotypic directions. Emond explains that it:
uses partially estimated weights for the variants and can also detect genes with different variants that have opposing effects on the phenotype
- Ran 10 million MZ bootstrapping iterations (see p. 10 and p. 25 of the supplement). MZ stands for Morris and Zeggini, but I’m not clear how MZ bootstrapping is different from regular old bootstrapping. This is the one thing Emond doesn’t completely explain, even in the supplement.
- Screened DCTN4 by Sanger sequencing (what it is, why it’s still used) in 696 additional individuals with CF. (Though this appears here as a bulletpoint alongside the additional statistical tests, it is clearly a LOT more important and was also surely the most time-consuming aspect of the validation).
- Performed Cox regression and created Kaplan Meier survival curves (see Fig1b-d and Online Methods in the main paper) stratified on the age that the patients were each enrolled in the study, to rule out as a source of error the fact that someone’s P. aeruginosa infection status might affect their enrollment status.
- Re-ran RVT1 on only the patients of European ancestry (whom they identified using principal component analysis rather than self-identified ethnic group; see p. 16-17 of the supplement) in order to rule out bias from different allele frequencies in different ethnic groups.
- Created Kaplan Meier survival curves separately for each genotype (the two variants, hetero- or homozygous) to determine the relative severity of phenotype associated with each genotype as well as for mucoid infection (as opposed to age of infection) as the phenotype.
Emond also quality controlled on the front end, with the usual list of measures– throwing out variants with low call quality (coverage <5) , far out of Hardy-Weinberg equilibrium, etc. (it’s all in the online methods). And to top it all off, the paper concludes with an excellent discussion of the biological relevance of Dynactin 4, the protein encoded by DCTN4: evidently it’s got a well-established role in autophagy, and autophagy has got a well-established role in clearing P. aeruoginosa infections.
In the conclusion, Emond writes:
To our knowledge, this is the first study to discover a gene for a complex trait, or at minimum a genetic modifier of a Mendelian trait, using exome sequencing and an extreme phenotype study design.
Let’s hope it’s the first of many.