How (and why) to create population covariates using 1000 Genomes data
This post aims to give step-by-step instructions on how to model and control for population stratification in a genetic association study by combining 1000 Genomes data with your own data.
In my case, I’ve got exome data from 50 patients and I have aligned it to the human genome and called variants using my GATK pipeline. Now I want to test for the association of genetic variation with a phenotype. To model the effect of individual variants, I can use PLINK (see tutorial; post forthcoming), and for a “gene score” model aggregating the effect of multiple rare variants by gene I can use my R implementation of RVT1 and RVT2. But in order to get meaningful results from either of these types of models, I will need to control for the effects of population stratification.
Before I get into any code, let me see if I actually understand the concepts here well enough to explain them.
We human beings are all related to each other — we all share common ancestors if you go back far enough. If some of the sample individuals in your dataset are more closely related to each other than to the others, this will bias the outcomes of all your models. In an imaginary world where it were possible to randomize an organism’s genotype and then read out a resulting phenotype, it would be pretty easy, given enough iterations, to pin down the variant(s) that cause the given phenotype. But we don’t inherit genetic information randomly. For each chromosome, each of us gets one copy from our father and one copy from our mother. There is some amount of crossover, but for two loci A and B that are close to one another, odds are that if I have my mother’s mother’s variant at A and my sibling has my mother’s mother’s variant at A, we probably both have our mother’s mother’s variant at B too. These two variants are on the same haplotype and my sibling and I both got that haplotype from my mother who got it from her mother.
By comparing at how many loci me and another person share 2, 1, or 0 of our alleles, you can figure out whether we are closely related. Identical twins should share both alleles at 100% of loci. Siblings should share 2 alleles at 25% of loci, 1 allele at 50% of loci and 0 alleles at 25% of loci. Parent and child should share 1 allele at 100% of loci. Half siblings should share 1 allele at 50% of loci and 0 alleles at the other 50%. This phenomenon is called identity-by-descent (IBD). The “identity” in this term refers not to who people are but to the exact match of one person’s allele to another’s, as in the sentence “these two sequences exhibit 100% identity”, not the sentence “insert a credit card to verify your identity.” Two people’s identity-by-descent, then, is the amount of genetic information they share because they got it from the same ancestor.
But notice that this breaks down pretty quickly. Above I said that parent and child should share 1 allele at 100% of loci. In reality the parent and child might well share 2 alleles at many loci just by chance, because one parent happened to have the same variant as the other parent. So we can’t measure IBD directly. Instead we have to first measure something simpler and easier to quantify: identity-by-state (IBS), which simply means “at how many loci do these two people share 2, 1, or 0 alleles”, without making any claim as to why they they share those alleles. Note that IBS and IBD are not opposites or opposed in any way. IBS just means “how much genetic information is the same” and IBD means “how much genetic information is the same because of recent shared ancestry“.
A moment ago I mentioned that one parent might “happen” to have the same variant as another parent. But what does “happened” really mean here? In many cases it means that the two parents also got the variant from the same ancestor (though it could also be by separate chance mutations). So the more recent the parents’ common ancestor, the more loci at which they will share variants. This will be relatively few loci for an interracial couple, relatively more loci for parents of the same ethnicity, and a whole lot of loci if the parents are part of the same extended clan, which is to say, third or fourth cousins or something. Because we all have common ancestors you might be tempted to think of everyone’s relation to everyone else in terms of IBD, but at some point that ceases to make sense because of two genetic forces at work. (1) Crossover will gradually mash up haplotypes so that, even if two people with many of the same ancestors share a lot of variants, they don’t share them in the same contiguous tract on one haplotype. As more and more generations pass, allowing more opportunities for crossover, and absent other confounding forces, two loci are said to move towards zero linkage disequilibrium. (2) Mutations will gradually make it so that even tracts of haplotype you still have intact from your great great great grandmother no longer exhibit perfect identity to the haplotype she had, or that her other descendents have today. And if there’s no “identity,” there cannot be said to be “identity-by-descent”.
We can measure IBS pretty easily, though there’s a little bit of a wrench even here. When you call variants with GATK, samtools, etc. you will get a genotype for every sample at any locus where any sample differs from the reference genome you’re using. So for two samples that are quite similar, you may not even know just how similar if you didn’t even call genotypes at all the potential variant loci where they were the same. I am still trying to figure out whether / how much of an issue this is. In any event, as long as you called variants on a number of samples together, it seems you’re probably fine.
So once you know the number of IBS-0, IBS-1 and IBS-2 loci between two individuals, how do you compute IBD? It’s not simple. PLINK [Purcell 2007] uses a maximum likelihood estimator described in [Milligan 2003]. After reading this I am still not sure I fully understand the approach, but let me talk through at least one important concept here. You can imagine that estimating IBD will depend upon allele frequency. Given that two people share an allele, that allele’s frequency in the population determines the relative likelihood that these two people share it by chance versus by ancestry. So the computation of IBD may be understood as computing the amount of genetic information that is shared in excess of the amount expected to be shared by chance. Allele frequency is a tricky thing, though, because it varies according to what you consider to be the reference population. Consider a biallelic SNP with alleles A and a. In ethnic group #1, allele frequencies are A: .99, a: .01 and in ethnic group #2, allele frequencies are A: .01, a: .99. If I analyze a sample that is half ethnic group #1 and half ethnic group #2, then my overall allele frequency is 50/50. I then compute IBD and find that two individuals from ethnic group #1 share the AA genotype (thus IBS-2). Imagine other loci with the same dispersion of allele frequencies: B vs. b, C vs. c, etc. I will tend to incorrectly find that two individuals from the same ethnic group have more IBS-1 and IBS-2 than would be expected by chance, when in fact their amount of IBS-1 and IBS-2 is perfectly likely given the allele frequencies in that population. For this reason, PLINK recommends only calculating IBD “in a homogeneous sample.” They never say what “homogeneous” means. How homogeneous? Is all Italians good enough or do they have to be all Tuscans? My interpretation of PLINK’s advice is that you should calculate IBD on relatively homogeneous subsets of your data, subsetting to the extent practical given your sample size. That, in turn, requires knowing what subsets of your sample individuals are ethnically similar.
Modeling the population substructure or ethnic grouping of your sample individuals can be done by computing the IBS distance between each pair of individuals and then plotting (to get a sense visually) or clustering (to actually generate covariates you can use in a model). Conceptually, if you have 100,000 loci, what you’re really doing is plotting the individuals as points in a 100,000-dimensional space where each individual’s distance from another along each axis is either 0, 1, or 2 (i.e. IBS-0 is a distance of 2, IBS-1 is a distance of 1, IBS-2 is a distance of 0). Then you are computing the distance between each pair of points using the Pythagorean theorem: distance = square root of the sum of squared distance along each axis. Those distances will only plot properly in a 100,000-dimensional space, but, with higher dimensions being difficult to visualize and all, we can use multi-dimensional scaling to plot an approximation of the distances in 2D (i.e. we can iteratively try to find a positioning of the points in two dimensions that minimizes conflict between their true distance and their distance as plotted).
If you just do this sort of multi-dimensional scaling on your own samples (and I’ll talk through how to do it in a minute), you will get a plot that looks something like this:
Which, when you think about it, is not really that helpful. Because this is multi-dimensional scaling, the axes are not meaningful and we have no sense of scale. Is that person down in the bottom left corner from a different village than the others or from a different continent than the others? Can these people all be treated as one group in your analysis or is there significant substructure here that we should be controlling for? There are also no labels. Which group corresponds to which ethnicity or population? If you were actually to find a variant associated with phenotype in your study, the first question everyone will ask is whether it might be caused by population substructure, i.e. whether your cases were enriched (vs. controls) for some population in which that variant has a higher frequency than other populations. And you can actually browse allele frequencies in (very coarsely grouped) populations using the 1000 Genomes browser — for instance, for rs4665058, a SNP associated with heart attack risk, you can see some allele frequencies here – if you know the populations your samples come from.
In order to get some figurative “signposts” on this plot, we need a curated public database of human genetic variation. Enter 1000 Genomes. As of today they seem to be up to almost 3,000 individuals from 26 populations (though it looks like not all the more recent data are public yet since it comes in discrete releases rather than as a trickle of new samples sequenced). By combining your data with 1000 Genomes and plotting them together, you can tell what population each of your samples is genetically nearest to, and how meaningful the differences are between them.
Let’s get started.
step 1. download 1000 Genomes data and subset the variants you want
Looking at the data release page, you’ll see that variant calls (i.e. VCFs), alignments (i.e. BAMs) and raw reads (i.e. FASTQs) are all available. For our purposes, you only need variants. Because 1000 Genomes is such a huge amount of data to work with, I also made the decision to use the August 2010 release which has just 629 people in it. It represents most of the populations included in subsequent releases, and there are at least a couple of populations each for Africans, Asians, Europeans and Latin Americans.
(Aside: the newer May 2011 release has 1092 people, including 2 new populations not in the August 2010 release (Iberian Spanish IBS and Colombians in Medellin CLM) but I ultimately decided it was not worth the trouble for now. My step 2 (below) wouldn’t work with that vcf file because it’s large enough that, in --plink mode, vcftools throws an error Could not open temporary file. Most likely this is because the system is not allowing me to open enough temporary files. Try using ulimit -n to increase the number of allowed open files. even though ulimit was set to unlimited, and in --plink-tped mode, vcftools ran forever, producing an arbitrarily large TPED file as it went (it got up to 300GB before I killed it, from a 5 GB VCF file).)
1000 Genomes is whole genome data, and I’m just working with exome. Moreover, given the large number of samples, they’ll have called variants at a lot of exonic sites where I did not observe a variant. So 1000 Genomes has a lot more variants (i.e. rows in the VCF file) than I need in order to compare 1000 Genomes with my data. I tried a few different ways of getting just the data I needed, and let me tell you what didn’t work so you don’t make the same mistake. First I wrote a script to walk through my own VCF file and use tabix as described here to query from NCBI only the variants present in my samples. This worked well for a while, at a rate of about 0.3 variants per second, until the server started rejecting my requests and the rest of my jobs failed. So instead I just downloaded the whole VCF file from NCBI:
wget ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/release/20100804/ALL.2of4intersection.20100804.genotypes.vcf.gz
Which worked just fine and took about 3 hours. Then I modified my script to query the local file rather than the copy on NCBI’s server and I create a hundred-odd jobs to subset out the desired variants. This, too, failed, I suppose because I had too many processes trying to access the same file at once. So finally I gave up on parallelizing it and just ran one job overnight to subset all the variants from my VCF file out of the 1000 Genomes file. Here’s the Python script, though if I had known from the outset I’d be doing it in serial, it probably could be done more easily with vcftools:
import sys
import os
from time import time
# location on the web:
# ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/release/20100804/ALL.2of4intersection.20100804.genotypes.vcf.gz
if(len(sys.argv) <> 2):
print "usage: python get-1000g.py vcffilename.vcf" # vcffilename.vcf is your VCF file listing the sites you care about
infilepath = sys.argv[1]
infileprefix = infilepath.split(".")[0]
infile = open(infilepath,"r")
outfilepath = "1000g_" + infileprefix + ".vcf"
kgvcfpath = "~/1000g/ALL.2of4intersection.20100804.genotypes.vcf.gz" # 1000g vcf file
clcall = "tabix -H " + kgvcfpath + " > " + outfilepath # -H gets just the header
os.system(clcall)
counter = 0
starttime = time()
for line in infile.readlines():
if(line[0]=="#"):
continue
col = line.split("\t")
chromosome = col[0][3:] # strip "chr" from front
position = col[1]
clcall = "tabix " + kgvcfpath + " " + chromosome + ":" + position + "-" + position + " >> " + outfilepath # >> appends rather than overwriting
os.system(clcall)
counter += 1
if(counter%100==0):
rate = counter / (time() - starttime)
print "processed " + str(counter) + " lines at an average rate of " + str(rate) + " lines per second"
This took about 4 hours to get 180,000 variants out of the 629 genomes in the August 2010 release of 1000 genomes, a rate of about 15 variants per second.
(By the way, I also tried converting the 1000 Genomes VCF to PLINK format first and then subsetting it; this was much, much slower.)
step 2. convert 1000 Genomes and your data to PLINK format and combine them
At this point you’ve got two files, we’ll call them 1000g_myvariants.vcf, which has columns for the 629 1000 Genomes people and rows for each variant observed in both 1000 Genomes and in your sample, and myvariants.vcf which has columns for your samples and rows for each variant you called. At some point you will need to merge these so you’ve got one file with both sets of individuals and only the intersection of the two sets of variants called. Don’t do this with vcf-merge. For me, at least, this set all of my samples’ genotypes to ./., which I suspect is because 1000 Genomes variants are phased while mine were not. Instead, convert each VCF file to PLINK format first and then manipulate them.
To convert:
vcftools --gzvcf 1000g/1000g_myvariants.vcf.gz --plink --out 1000g # 70 seconds vcftools --vcf myvariants.vcf --plink --out myvariants # 12 seconds
At this point, you may find that you still cannot combine the two files because 1000 Genomes, which uses GRCh37, lists the chromosomes as 1, 2, etc. while if you used hg19, you have them listed as chr1, chr2, etc. If so, you can simply strip the first three characters from each line of your .MAP file using sed:
sed 's/^...//' myvariants.map > myvariants.fixed.map rm myvariants.map mv myvariants.fixed.map myvariants.map
Now, you already subsetted the 1000 Genomes data to include only your variants, but you didn’t yet subset your data to include only the variants found in 1000 Genomes. To do that, we’ll need to create a list of variants to include (PLINK refers to this as ‘snplist’ in the data management documentation, so I will too, even though it does include indels as well). On the way we’ll also fix some other problems. First, for variants with no dbSNP id, i.e. no rs_______ number, vcftools fills in their name as their base number on the chromosome, but without the chromosome number. So if there are unnamed variants at the same address on different chromosomes, PLINK interprets them as duplicates. Since I have plenty of variants, I handle this by using only the variants with a dbSNP id. This line of code pulls all the lines containing ‘rs’, cuts out the second column (the SNP column, i.e. the variant name) and puts it into a new file:
grep rs 1000g_myvariants.map | cut -d $'\t' -f 2 > rs.snplist.raw
Or better still:
grep -o 'rs[0-9]*' 1000g_myvariants.map > rs.snplist.raw
If you try to run PLINK on this snplist, you’ll find you still have some problems. There are duplicate marker names, and I never figured out why this is, but again, assuming I have enough variants that I’ll be fine anyway, I just got rid of them by sorting and removing duplicates:
sort rs.snplist.raw | uniq > rs.snplist.dedup
Even this still didn’t work: when I tried to extract these SNPs and combine the 1000g files with my variants, PLINK gave me the following error:
Found 107 SNPs that do not match in terms of allele codes Might include strand flips, although flipped A/T and C/G SNPs will be undetected) Writing problem SNPs to [ all.missnp ]
So then I went back and removed those problem SNPs too:
plink --file myvariants --extract rs.snplist.dedup --exclude all.missnp --recode --out myvariants.subset plink --file 1000g_myvariants --extract rs.snplist.dedup --exclude all.missnp --recode --out 1000g_myvariants.subset
And finally PLINK ran without error and created the output files. I then combined those using --merge:
plink --file 1000g_myvariants.subset --merge myvariants.subset.ped myvariants.subset.map --recode --out all
step 3. calculate pairwise IBS and IBD
Recall that IBD depends upon allele frequency. You’re supposed to compute it only on a relatively homogeneous sample, and we can come back later and make sure we do that. For now let’s operate on the assumption that your sample is homogeneous, and if that turns out not to be true we can fix it later. First, calculate allele frequencies for just your samples (not 1000 Genomes):
plink --file myvariants.subset --freq --out myvariants
This creates a file myvariants.frq which you will need in a moment.
Now we want to calculate the IBS and IBD between every pair of samples. If you have 50 samples and are using the 629 1000 Genomes people from August 2010, you’ve got 679 samples, thus 679 choose 2 = 230,181 pairs. That’s a lot of pairs so let’s parallelize by taking blocks of 100 samples to compare to each other, thus 10,000 comparisons per job. Create text files with the first two columns of your all.ped file, 100 lines per text file:
cut -d ' ' -f 1,2 all.ped | split -d -a 3 -l 100 - tmp.list
Then create jobs using this bash script, barely modified from that suggested on the PLINK website:
# jobs will be under 1 minute each, can submit to short queue
let i=0 a=6 # a is number of files created by the above step, minus 1
let j=0
while [ $i -le $a ]
do
while [ $j -le $a ]
do
bsub -q short -o /dev/null -e /dev/null plink --file all --read-freq var06.frq\
--all \
--genome \
--genome-lists tmp.list`printf "%03i\n" $i` \
tmp.list`printf "%03i\n" $j` \
--out data.sub.$i.$j
let j=$j+1
done
let i=$i+1
let j=$i
done
These jobs will run in about 1 minute each. If, like me, you forgot to specify the short queue on the first try and your jobs are pending and pending, you can change them all to the short queue with this line:
bjobs | cut -d ' ' -f 1 | grep -v JOBID | awk '{ print "bmod -q short " $0 }' | bash
Anyway, once the jobs are done, recombine the files into a single .genome file as such:
head -1 data.sub.0.0.genome > header cat data.sub.*.genome | grep -v FID1 | cat header - > all.genome
And spot check that you did this right by counting lines:
wc -l all.ped wc -l all.genome
If the first answer is n, the second one should be (n choose 2) + 1, so n(n+1)/2 + 1. (The +1 is for the header.)
step 4. create an MDS plot to visualize the data
Now that you have your .genome file, you can very quickly create a multi-dimensional scaling plot in 2 dimensions using PLINK:
plink --file all --read-genome all.genome --cluster --mds-plot 2 --out all_mds_2
And then plot it in R with this bit of code:
setwd("/your/path/here/1000g")
m <- as.matrix(read.table("all_mds_2.mds"))
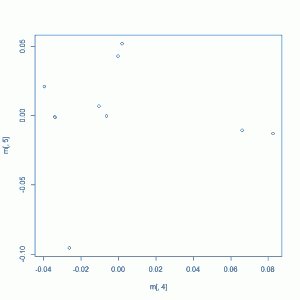
plot(m[,4],m[,5])
Your plot might look something like this (this example plot was created using only the 1000g people and not my samples):
Which starts to give us more of a sense of the population groupings. What would be even more awesome is to have coloring so we know which group of points is which population. This is a little bit of a pain, since the population identifiers in 1000g are only specified in a non-database-compatible Excel file. Open the Excel file, strip off the explanatory stuff at the top so you have just the table, rename the ‘Type’ column to get rid of the line breaks in it, then read both that and your MDS plot file into PostgreSQL with this SQL code:
drop table if exists kg_metadata;
create table kg_metadata(
population varchar,
sra_individual_sample_accession_number varchar,
coriell_sample_id varchar,
family varchar,
gender varchar,
relationship_ varchar,
type__unrel_duo_trio_ varchar,
whole_genome_center_for_full_project varchar,
exome_center_for_full_project varchar,
pilot_1_center varchar,
pilot_2_cener varchar,
pilot_3_center varchar,
has_omni_genotypes varchar,
has_axiom_genotypes varchar,
has_more_than_3x_aligned_coverage_at_omni_sites varchar,
has_more_than_70__of_exome_targets_covered_to_20x_or_more_ varchar);
copy kg_metadata from '/your/path/1000g/20111108_1000genomes_samples.csv' with csv header;
drop table if exists all_mds_2;
create table all_mds_2(
fid varchar,
iid varchar,
sol varchar,
c1 varchar,
c2 varchar);
copy all_mds_2 from '/your/path/1000g/all_mds_2.mds.csv' with csv header;
(Note: PLINK outputs fixed width, not delimited files, so you’ll need to convert first before reading in.)
Then go back to R and create a database connection, get the MDS plot data along with the population identifiers, and plot them. Here’s an example plotting only the 1000g people and not my own samples:
library(RPostgreSQL) # first load package RPostgresql
drv <- dbDriver("PostgreSQL")
readcon <- dbConnect(drv, dbname="mydb", user="postgres", password="password")
readsql <- "select k.population, mds.c1, mds.c2 from kg_metadata k, kg_only_mds mds where k.coriell_sample_id = mds.fid order by mds.fid;"
rs <- dbSendQuery(readcon,readsql)
tbl <- fetch(rs,n=-1)
k = rainbow(n=length(unique(tbl$population)),s=1,v=.7,alpha=1) # create a color map for the unique populations
l = unique(tbl$population) # get the names of the populations for the legend
plot(tbl$c1,tbl$c2,col=k[factor(tbl$population)]) # create the plot
legend("topright",l,col=k[factor(unique(tbl$population))],cex=1.0,bty="n",pch=19) # add the legend
dbDisconnect(readcon)
dbUnloadDriver(drv)
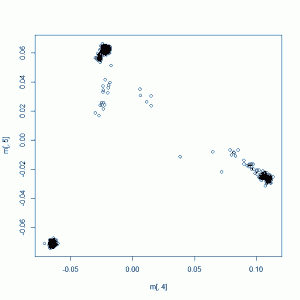
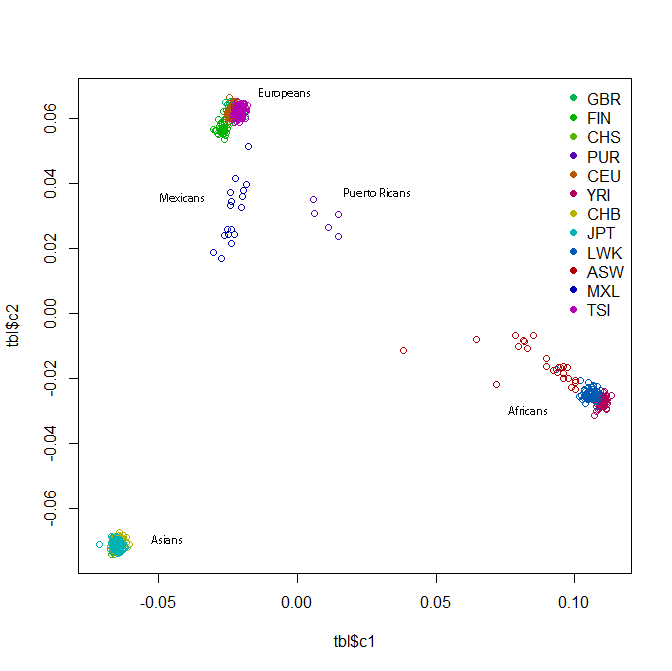
This should give you a plot something like this:
The readability of this plot is somewhat less than ideal because there are too many colors, the points overlap each other and also because I also don’t fully understand R or how to create color maps in it. I added some labels to supplement the legend. All the clusters have a lot of overlap, but within the African cluster, you have the Yoruba on the far right, then the Luhya, then the Americans of African descent stretching towards the middle of the plot. The Europeans have the Tuscans on the right, then the European-Americans, then the Brits and Finns on the left. In the Asian cluster you can see the Beijing Chinese a bit more on the right, the southern Chinese towards the bottom of the cluster, and the Tokyo Japanese a bit further left.
If you wanted to zoom in on one part, you can re-plot specifying the x and y limits:
plot(tbl$c1,tbl$c2,col=k[factor(tbl$population)],pch=20,xlim=c(-.08,-.05),ylim=c(-.08,-.06)) # zoom in on the Asian cluster
Or, to do it right, you can regenerate the plot from PLINK with just those groups included (which would give you a different answer, since there are now a different set of distance constraints that the multi-dimensional scaling algorithm has to optimize against).
To plot the 1000g people along with your own samples (of unknown population, hence labeled ‘XXX’), just tweak the SQL query:
select coalesce(k.population,'XXX') as population, mds.c1, mds.c2 from kg_metadata k right outer join all_mds mds on k.coriell_sample_id = mds.fid order by mds.fid;
Hopefully this will be informative and will give you an idea of just how different of populations your samples come from and whether / to what extent you need to control for their population substructure.
update 2012-10-25: the method described here can introduce some bias by enriching rare variation in your sample relative to 1000G. see Population Substructure, Part II for how to handle this.
step 5 – clustering, or maybe not
One way to control for population substructure in PLINK is to cluster your samples. This is covered in a nice amount of detail in the PLINK tutorial. I’ll talk through how to do this first, then I’ll discuss why I don’t think this is the best way to control for substructure. The basic structure of the command line call for creating clusters looks like this:
plink --file all --read-genome all.genome --cluster --ppc .01 --out cv1
Where --ppc .01 means “put any two individuals in the same cluster unless you can reject at the .01 threshold the null hypothesis that they are from the same population.” So if you specify a higher threshold, say, .1, you’ll get more clusters, and if you specify a lower threshold, say, .001, you’ll get fewer clusters. With 1000 genomes, though, even at ppc = .0001, you’ll still get a lot of clusters. There are different ways to constrain the clustering solution as described in PLINK documentation as well: --K 10 means “give me exactly 10 clusters”, --cc means “make sure every cluster has at least one case and one control” (this makes your clusters more informative in your model; you need to add phenotype to your PED file, which we haven’t done yet here), --mc 20 means “give me clusters of up to 20 people.”
Supposing you’ve got a clustering solution you think is workable, you can then put that solution into your association analysis in PLINK. Your association analysis will not include the 1000 Genomes people, so just clip off the part of the clustering solution you need (hopefully your samples are named such that they all fall at the beginning or end of the list). I give the cluster file a descriptive name so I can remember what parameters I used to create it, for instance:
tail -50 cv1.cluster2 > MC50.cluster2
A possible command line call to do association analysis within these clusters would be:
plink --tfile variants --no-parents --1 --maf .05 --geno .10 --within MC50.cluster2 --mh --adjust --out analysis2
Note: to use the --within option correctly, you must specify either --mh or --mh2 as the analysis type. Conceptually this is because PLINK uses the Cochran-Mantel-Haenszel test for stratified analysis, which is basically a χ2 test repeated for each cluster. If you do not specify --mh, then PLINK will still load your clusters and will even tell you it’s doing so with a message like Reading clusters from [ MC50.cluster2 ] 50 of 50 individuals assigned to 2 cluster(s), yet it will not actually use the clusters in its analysis. You can tell that this is the case by comparing the results to the results you got with the same command without the clusters. They’ll be identical. Now, if you have a small enough a small number of samples that you’d like to use Fisher’s exact test instead of χ2, I discovered that PLINK will allow you to specify both parameters, i.e. --mh --fisher, and will produce a file like analysis2.cmh.fisher.adjusted which appears to be the results of a CMH test but with Fisher instead of χ2, though this option is not called out the stratified analysis documentation so I am not 100% sure I trust it.
Now, when you ran this PLINK analysis without clustering, you probably saw a message like this:
Genomic inflation factor (based on median chi-squared) is 1.33049 Mean chi-squared statistic is 1.16691
Genomic inflation means that the total amount of statistical significance coming out of your model is more than it should be — variants are systematically showing up as more associated with phenotype than would be expected by chance. If you QQ plot the p values from such an analysis, you’ll find many dots above the diagonal line. What you want is everything on or about the line, except for the 1 (or 2 or 3) variants that are actually causal, which (if they exist) will be high above the line. After you control for population substructure by using the clusters you created above, the hope is that you’ll see this:
Genomic inflation factor (based on median chi-squared) is 1 Mean chi-squared statistic is 1
Which would mean that your clusters successfully captured all of the population substructure present in your samples. More realistically you’ll see numbers that are closer to 1 but not quite 1.
So that’s how to use PLINK to do association analysis within clusters. Again, there’s much more detail in the PLINK doc section on stratified analysis. But I’m not a big fan of this sort of analysis, mostly because the clustering seems so arbitrary, or at least, I don’t know enough about it to wield it effectively. The --ppc, --K, and --mc options all require you to specify some number, and you’ll get very different results depending on what you pick, which makes me nervous. And I haven’t found a good way to constrain the clustering to be analytically meaningful for my samples. If you run clustering on just your small set of samples, you have no benchmark– are these people different enough to deserve 2 clusters, or 10? And yet if you combine with 1000 Genomes and then cluster, the clusters won’t necessarily break up your samples in any way that’s actually helpful for reducing genomic inflation. Your samples might all be in one cluster, or all in one except for one outlier. I also find that the clusters don’t always correspond well to what I see on my MDS plot. Perhaps that is to be expected since MDS is, after all, an imperfect representation of distances that cannot be properly plotted in 2 dimensions. Still, when I plot my data with 1000 Genomes and see clearly that some people fall into population A and others into population B, and then the clustering does not divide them on these lines, it makes me skeptical — at least, skeptical of whether I know enough to use clusters effectively.
So instead of using discrete clusters, I prefer to control for population substructure using continuous-valued covariates as described in steps 7-8.
step 6. IBD analysis to detect related samples
Before you get into using covariates in our analysis, you should use IBD calculations to check the relatedness of people in your sample. At the end of step 3, you created a file all.genome which contains IBD figures for all your samples (and all of 1000 Genomes). Let’s read that into SQL (PLINK outputs it as fixed width, so you’ll need to convert to CSV first):
drop table if exists genome;
create table genome(
fid1 varchar,
iid1 varchar,
fid2 varchar,
iid2 varchar,
rt varchar,
ez varchar,
z0 numeric,
z1 numeric,
z2 numeric,
pi_hat numeric,
phe integer,
dst numeric,
ppc numeric,
ratio numeric);
copy genome from '/your/path/here/all.genome.csv' with csv header;
Recall that each row represents one pair of individuals. The z0, z1, and z2 fields tell you at what fraction of loci that pair of individuals are estimated to share 0, 1 or 2 alleles by descent. Here are some patterns to look for:
| Relationship | z0 | z1 | z2 |
| Duplicated sample or identical twins | 0.0 | 0.0 | 1.0 |
| Parent/child | 0.0 | 1.0 | 0.0 |
| Siblings | 0.25 | 0.5 | 0.25 |
| Half-siblings | 0.5 | 0.5 | 0.0 |
| Grandparent/grandchild | 0.5 | 0.5 | 0.0 |
| First cousins | 0.75 | 0.25 | 0.0 |
And so on (more comprehensive table from UC-Davis). Of course it will be fuzzier in this both due to sequencing errors and due to biological noise (hemizygous deletions, de novo mutations, etc.) But if you see a 0 / 0.02 / 0.98 spread, you can be pretty sure it’s a twins-or-duplicate-sample scenario. Most researchers seem to remove one of the two from their study when this happens. As for the other relationships, what you do depends on what you expected going in. If you had pedigree information, take this as validation of it– were the samples labeled correctly? Any non-paternities? If you had no pedigree information, now you can construct some of it. If you find relationships you didn’t know were there, your effective sample size and variance are now smaller than you thought, because two of your individuals are correlated with one another (see Risch & Teng 1998). If you have multipled affected pairs of siblings, this lends itself to a whole different sib-pair study design which can help you to narrow in on the causal locus (see Kerber 2008).
It’s likely, though, especially if you created your genome file by combining your data with 1000 Genomes as I’ve done above, that you get inflated results, where it looks like a lot of people are related to each other, with lots of pairs having z1 and z2 figures in the .2 or .3 range. 1000 Genomes has known related samples in it (all denoted in the spreadsheet), so you can use those to spot check whether your values seem to call relationships correctly. If not, it’s because you have too much population heterogeneity in the dataset. You’ll still be glad you created all.genome as you needed it for the MDS plot which you in turn need for steps 7-8, but in order to be sure you’ve calculated IBD correctly, you will want to go back and re-run IBD (i.e. PLINK --genome, the beginning of step 3) multiple times for different relatively homogeneous groups within your sample, using each one’s own allele frequency. To create the homogenous groups, you could use clusters that you got from step 5. (As I said, I am skeptical about some of the clusters that PLINK generates, but I haven’t come up with a better way to do this).
update 2012-10-25: see Population Substructure, Part II for detailed instructions on how to select homogeneous subsets to detect familial relationships.
step 7. plink analysis using covariates
What you did by creating a 2-dimensional MDS plot in step 4 was to find values on two dimensions which best capture the genetic variation. That’s kind of like principal component analysis. Now, for purists, these two methods are not necessarily the same, unless you do MDS with Euclidean distance — see relevant StackExchange discussion. The PLINK paper claims that PLINK offers an option to use Euclidean distance: “There is an option to use a Euclidean IBS distance metric in place of the standard metric of proportional sharing; classical MDS based on a Euclidean distance metric is numerically identical to principal-components analysis, which forms the basis of other methods” [Purcell 2007], but it appears that this is no longer actually supported in PLINK — the MDS documentation simply states that “standard classical (metric) multidimensional scaling is used”. So if you’re a purist (or your reviewers are), you can do a true PCA in R.
But assuming for the time being that you’re not a purist, you can use c1 and c2, your MDS plot dimensions, as covariates in any model you want to do. If you think there’s room in your model for three covariates, you can re-run it with --mds-plot 3.
In this step, we’ll use the covariates in PLINK. Now, much as you need to use --mh if you want to use clusters, only some types of PLINK analysis allow the use of covariates. Remember that PLINK’s default test for significance is χ2 and that this, as well as other options such as Fisher’s exact, test only categorical variables: are the two genotypes more unevenly distributed across the two phenotypes than would be expected by chance? There’s no room in such an analysis for continuous variables such as your c1 and c2. Instead you’ll need to do either logistic or linear regression.
First, get your covariates into a separate text file that you can tell PLINK to read. If you have your MDS plot values in SQL, copy them out as such: (I used a regex to get only the numeric iids, i.e. to include my samples and exclude the 1000 Genomes samples).
copy ( select fid, iid, c1, c2 from all_mds_2 where iid ~ '^[0-9].*' order by fid, iid ) to '/your/path/here/mds2_covar.txt';
If you have a dichotomous phenotype, logistic is conceptually what makes more sense. From a statistical point of view, that is. From a biological point of view, not so much: logistic regression can’t handle linear separation, which means genotypes that segregate categorically by phenotype, which are probably the most likely causative genotypes, throw warnings and come out as insignificant– see detailed discussion in comments to the RVT1 post. If after reading that you still want to do a logistic regression, this will do the trick:
plink --tfile variants --no-parents --1 --maf .05 --geno .10 --covar mds2_covar.txt --logistic --adjust --out analysis3
If you’d rather do a linear regression, you’ll need to trick PLINK into thinking you have a quantitative phenotype. If you just use the --linear option with your regular dichotomous phenotype, PLINK will take matters into its own hands do a logistic instead of linear regression without throwing an error (other than naming the output file with a .logistic extension). To create a phenotype PLINK will recognize as quantitative, just use any value except 1 for the cases:
copy ( select sample_id, sample_id, phen_code::numeric * 0.5 from samples s order by sample_id ) to '/your/path/here/quantpheno.phe';
Then read that in as the phenotype and do a linear regression:
plink --tfile variants --no-parents --pheno quantpheno.phe --maf .05 --geno .10 --covar mds2_covar.txt --linear --adjust --out analysis4
step 8. gene score analysis using covariates
The same covariates you used for variant-level analysis in PLINK can also be used for gene score analysis, say RVT1/RVT2. In principle this is trivial: you just need to get those covariates into the same table as your input data for the RVT models and then include them as variables in your linear regression: model <- lm(tbl$phen_code ~ rini + c1 +c2) . For completeness I’ll include here the SQL and R code I used (slight modifications from the code in the RVT1/RVT2 post in order to include covariates):
-- create table of underlying data for RVT1 and RVT2 models
drop table if exists var06.rvt_data;
create table var06.rvt_data as
select rvgm.gene_name,
sv.sid,
s.phen_code,
sum(case when ((sv.variant_allele_count > 0 and rvgm.vaf < .125) or (sv.variant_allele_count < 2 and rvgm.vaf > .875)) and use_flag then 1 else 0 end)::numeric ri, -- number of rare variant loci where this sample has a rare variant
sum(case when use_flag then sv.alleles_genotyped else 0 end)::numeric/2.0 ni, -- number of rare variant loci genotyped for this sample
(mds.c1::numeric - norm.c1_av)/norm.c1_stddev c1,
(mds.c2::numeric - norm.c2_av)/norm.c2_stddev c2
from variants v, sample_variants sv, samples s, all_mds_2 mds,
(select e.vid, e.gene_name, coalesce(a.n1000g2012feb_all,0.0) vaf
from annovar_genome_summary a, effects e
where e.vid = a.vid
and (a.n1000g2012feb_all < .125 or a.n1000g2012feb_all is null or a.n1000g2012feb_all > .875) -- specify your MAF threshold in this line. I used 12.5%.
and e.effect_impact in ('MODERATE','HIGH') -- sepcify your inclusion criteria here
group by e.vid, e.gene_name, coalesce(a.n1000g2012feb_all,0.0)
order by e.vid, e.gene_name) rvgm, -- [rare variant]-[gene] match
(select avg(c1::numeric) c1_av, avg(c2::numeric) c2_av, stddev(c1::numeric) c1_stddev, stddev(c2::numeric) c2_stddev
from all_mds_2
where iid like '18%') norm
where v.vid = sv.vid
and sv.sid = s.sample_id
and v.vid = rvgm.vid
and mds.iid like '18%'
and s.sample_id = mds.iid::integer
group by rvgm.gene_name, sv.sid, s.phen_code, mds.c1, mds.c2, norm.c1_av, norm.c2_av, norm.c1_stddev, norm.c2_stddev
order by rvgm.gene_name, sv.sid
;
And:
library(RPostgreSQL) # first load package RPostgresql
drv <- dbDriver("PostgreSQL")
readcon <- dbConnect(drv, dbname="mydb", user="postgres", password="password")
writecon <- dbConnect(drv, dbname="mydb", user="postgres", password="password")
nsamples <- 50
readsql <- "
select gene_name, sid, phen_code, ri, ni, c1, c2
from rvt_data
order by gene_name, sid
;"
rs <- dbSendQuery(readcon,readsql)
writesql <- "
drop table if exists rvt1_results;
create table rvt1_results (
gene_name varchar,
lambda numeric,
p_value numeric
);
drop table if exists rvt2_results;
create table rvt2_results (
gene_name varchar,
lambda numeric,
p_value numeric
);
"
tmp <- dbSendQuery(writecon,writesql)
while (!dbHasCompleted(rs)) { # for each gene
tbl <- fetch(rs,n=nsamples) # get the data for the fifty samples
nonzero <- (tbl$ni != 0) # find the rows where ni is nonzero, i.e. the sample had at least one locus genotyped
tbl <- tbl[nonzero,] # restrict the analysis to rows where ni is nonzero
if(nrow(tbl) < .9*nsamples) next # only analyze genes where at least 90% of samples can be included
gene_name <- tbl$gene_name[1]
# RVT1
rini <- tbl$ri/tbl$ni # ri/ni
if (length(unique(rini)) != 1) { # skip monomorphic cases
model <- lm(tbl$phen_code ~ rini + tbl$c1 + tbl$c2) # you can add your xi vector of covariates to this model here
coeff <- summary(model)$coef["rini","Estimate"]
p_value <- summary(model)$coef["rini","Pr(>|t|)"]
writesql <- paste("insert into rvt1_results (gene_name,lambda,p_value) values('",gene_name,"',",coeff,",",p_value,");",sep="")
tmp <- dbSendQuery(writecon,writesql)
}
# RVT2
Iri <- 1*(tbl$ri > 0) # indicator variable for whether any rare variants are present. multiplying by 1 converts boolean t/f to integer 1/0
if (length(unique(Iri)) != 1) { # skip monomorphic cases
model <- lm(tbl$phen_code ~ Iri + tbl$c1 + tbl$c2)
coeff <- summary(model)$coef["Iri","Estimate"]
p_value <- summary(model)$coef["Iri","Pr(>|t|)"]
writesql <- paste("insert into rvt2_results (gene_name,lambda,p_value) values('",gene_name,"',",coeff,",",p_value,");",sep="")
tmp <- dbSendQuery(writecon,writesql)
}
}
dbDisconnect(readcon)
dbDisconnect(writecon)
dbUnloadDriver(drv)
reflections
Congratulations! If your genomic inflation factor from PLINK is closer to 1 and your QQ plot looks more straight and diagonal, then you have successfully controlled for much of the population stratification present in your sample. Odds are that your reward for this is that the promising leads you thought you saw are no longer statistically significant. Hey, at least you realized that before you tried to publish it.