Heritability and genetic modifiers in Mendelian diseases
A Mendelian disease is one where a single genetic mutation decides whether you get the disease or not. For instance, PRNP mutations are wholly responsible for fatal familial insomnia, and CFTR mutations are wholly responsible for cystic fibrosis.
By contrast, complex traits and complex diseases are determined by a whole bunch of different genetic factors. Height, for instance: if your parents are tall, you’re likely to be tall too, but it’s not as simple as ‘you got the tall gene.’ Though we don’t know the full genetic architecture of any complex diseases, it is believed that hundreds of genomic loci contribute to many complex diseases as well – such as schizophrenia (I couldn’t find any good recent reviews; one relevant paper is International Schizophrenia Consortium 2009).
The concept of ‘heritability’ is pretty simple for Mendelian diseases themselves because they follow Mendelian inheritance. If the disease is dominant, then an affected person’s kids are 50/50 to have the disease too, and if the disease is recessive then each child of two heterozygous carriers has a 25% chance of having the disease. For complex traits and complex diseases, a great deal of effort goes into trying to figure out how ‘heritable’ they are – how much of the phenotypic variance in the population can be explained by genetics, as opposed to environmental factors or stochastic variation (see heritability post).
However, even Mendelian diseases can have genetic modifiers, and those modifiers can be heritable. Cutting 2011 reviews what we know about genetic modifiers in cystic fibrosis. Even though everyone with both CFTR alleles gets cystic fibrosis, some people get very sick very young and others stay healthy much longer. Because cystic fibrosis is a loss-of-function disease, it can be caused by a wide variety of loss-of-function mutations in CFTR: Cutting says over 1800 mutations have been identified so far. Not surprisingly the biggest genetic modifier of many cystic fibrosis phenotypes (especially in the pancreas and intestines) – is simply which CFTR mutation(s) you have. Some are complete loss-of-function while others are able to preserve a little bit of functionality in some tissues.
However it has long been suspected that there are other genetic modifiers in cystic fibrosis as well. Cutting reviews a number of studies that have tried to estimate the heritability of some of the disease phenotypes (quantitative measurements of lung function, body mass index, etc.). The methods used are largely the same as the methods for estimating heritability in complex traits – MZ vs DZ twin studies, sibling correlation, etc. I didn’t get any sense of a consensus from Cutting’s article, though: the heritability estimates for cystic fibrosis phenotypes vary dramatically, all the way from 0.0 (the first MZ/DZ twin study found MZ twins no more similar than DZ twins for individual phenotypes, though there was heritability of one composite measure [Mekus 2000]) to 1.0 [Vanscoy 2007]. The only methodology new to me here was a study of phenotypic concordance between twins before and after they moved out of the home [Collaco 2010], a methodology purported to separate out the effects of shared vs. individual environment.
Cystic fibrosis is a bit of a special case: it is one of the most common Mendelian diseases. For more rare diseases you aren’t going to find enough twins to do twin studies. So I also spent some time looking at how heritability has been estimated in very rare diseases.
For prion disease, one study has suggested that age of onset has at least some heritability [Webb 2009]. Webb looked at three large pedigrees, each with a different mutation (6-OPRI CJD, P102L GSS and A117V GSS), and used parent-offspring regression to assess heritability of age of onset and age of death. Each of these 3 mutations has a different average age of onset, and for these particular mutations PRNP codon 129 genotype also matters: MV heterozygotes have later onset than MM or VV homozygotes. (Aside: as far as we know this is not true for FFI [Kong 2003]). Webb tried models with and without codon 129 genotype accounted for, because this information wasn’t available for some patients. Failure to include codon 129 genotype in models does add some noise, but it does not actually introduce any bias because as Webb points out, each mutation segregates with a particular allele such that the codon 129 genotype is entirely determined by the unaffected parent and therefore uncorrelated between affected parents and affected offspring. In any event, peoples’ ages of onset and death were Z-scored for each mutation, and then parents were regressed against offspring. If you look at the data, they don’t exactly scream correlation – here is Fig 4:
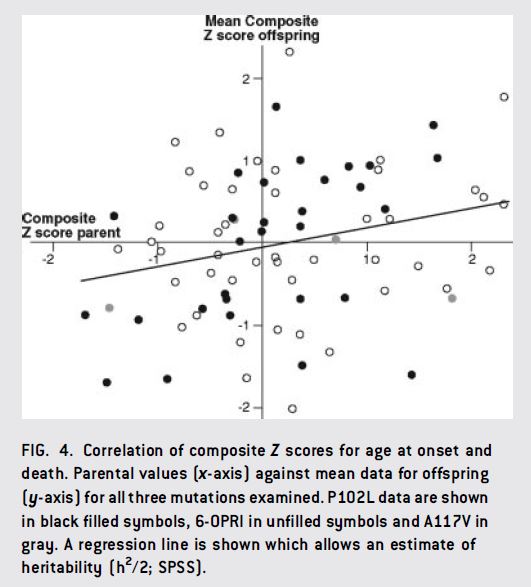
But apparently there was a global correlation with r = .25 – which, as I interpret it, would mean an upper limit on heritability of 2r = 50%. This correlation seemed to be driven mostly by the P102L cases (black dots in above), which had a significant r = .47, though the other mutations also trended towards correlation.
Squitieri 2000, studying Huntington’s Disease, has pointed out the risk of ascertainment bias in heritability studies examining age of onset. Imagine you’re recruiting patients for a study during a particular window in time, and you’re only considering patients who already have an age of onset, i.e. already have the disease. Only relatively concordant sibling pairs are going to be both available for the study at the same time – if two siblings are discordant, one will have already passed away or one will not yet have the disease at the time when the other one is enrolling in the study. The opposite is true intergenerationally: if you try to enroll parent-child pairs or trios, only parents with late onset and children with early onset will be available to enroll at the same time, and thus you’re selecting for discordant pairs. There are other issues too (early onset people are less likely to ever become parents, early onset children are likely to attract more notice and get enrolled in studies more often, etc.)
Because Webb’s study used parent-offspring pairs, it’s biased towards underestimating heritability if anything. Webb does not go into great detail about how the clinical data were processed and how/whether not-yet-affected carrier offspring were considered in the analysis, so it is hard to know how big an issue this might be.
Moving on, for prion disease in particular another source of evidence towards the existence of genetic modifiers is that scrapie incubation times vary about twofold between different inbred mouse lines [reviewed in Lloyd 2011]. This is no guarantee that there are similar modifiers in humans, but it’s fairly suggestive. Lloyd reviews several studies which have used mice for QTL mapping – a concept reviewed by Peters 2007. In brief, two inbred mouse lines are crossed to get highly heterozygous F1s, then the F1s are crossed again to get mixed F2s in which you can look for which genomic locations correlate best with the phenotype. For prion diseases these studies have revealed some candidate loci, but no conclusive modifier genes yet.
There is also some interesting literature on heritability of age of onset in spinocerebellar ataxia 2 (SCA2), which is caused by polyQ repeat expansion in the ATXN2 gene. Just like in Huntington’s Disease, the Q repeat length explains much of the variance in age of onset (more repeats is worse). So just like in HD, people who study SCA2 consider a residual age of onset – the difference between actual onset and predicted onset based on polyQ length. There are a number of other SCAs, each caused by polyQ expansion in a different gene, and Pulst 2005 (ft) hypothesized that some of the residual age of onset in SCA2 might be explained by polyQ length in the other SCA-causing genes. Pulst genotyped polyQ length in those genes in ~400 unrelated people and sure enough, it turned out that polyQ length polymorphisms in CACNA1A, the gene that causes SCA6, explained about 6% of the residual (not total) variance in age of onset in SCA2. None of the SCA2 patients had a CACNA1A allele long enough to cause SCA6 – but the early onset people had slightly longer alleles than late onset.
That’s quite an interesting finding and the results were significant even after Bonferroni correction. However, the heritability analysis in that paper was somewhat less awesome. The heritability calculations used a separate set of patients from the above analyses, and simply doubled the sibling correlation to obtain a figure of 55%. Pulst correctly describes this as an upper bound and not an estimate of heritability (no control to rule out shared environment contribution). But still, there is no control here for the ascertainment bias that Squitieri 2000 discusses – age onset studies are simply more likely to include concordant sib pairs than discordant sib pairs. If Pulst did anything to control for this problem, it’s not discussed in the paper – all it says about the sib pair data is that “For the analysis of residual variance and heritability, information from 148 SCA2 patients from 57 sibships was used.” This ascertainment bias will tend to inflate Pulst’s figure, so I would take 55% as a rather loose upper bound.
In myotonic dystrophy, the CTG repeat length explains most of the age onset variance. The repeat length also explains most of the level of somatic instability, but the residual instability explains part of the age of onset [Morales 2012]. Morales also suggests that the level of somatic instability itself is itself ~40% heritable, but here the analysis is not transparent. Morales feeds the data into QTDT, a software tool introduced by Abecasis 2000. Abecasis’ formula for partitioning variance into genetic, shared environment and individual environment components depends upon “the proportion of alleles shared identical by descent (IBD) between siblings j and k in family i” – to my reading, this is sibling IBD regression, similar to that used by Visscher 2006 in calculating height heritability. Visscher actually had genome-wide SNP markers to determine sibling IBD (which ranges from ~40% to ~60% – not all sibling pairs are equally alike!) Yet people have for years been using QTDT to do heritability estimates (both Morales above and U.S.–Venezuela Collaborative Research Project 2004) without any empirical sibling IBD estimates. Perhaps this involves an assumption that all sib pairs share 50% IBD, but if so, neither Morales nor the USVCRP paper mention this assumption, and it is not clear to me from Abecasis’ paper how the shared environment and genetic components can possibly be partitioned if IBD doesn’t vary at all. I also checked the QTDT online tour and, indeed, the variance partitioning relies on IBD from sibling pedigree files.
Maybe there is something I’m missing here (if so, please leave a comment to let me know) but, even after reading Abecasis 2000 and looking at the QTDT online tour, I am still at a loss for understanding how authors are using QTDT to create heritability estimates without any genome-wide SNP genotyping to determine IBD.
Heritability estimation is difficult to begin with [see Visscher 2008 for a review]. Doubly so in diseases that are too rare for twin studies to be possible, and doubly so again for age of onset phenotypes, where family studies suffer from often unexamined ascertainment bias. It is clear that some Mendelian diseases do have heritable modifiers of age of onset. Pulst 2005‘s discovery of a modifier for SCA2 is convincing and (to my knowledge) has never been contested in the literature; and Webb 2009‘s finding of heritability in prion diseases, because it uses parent-offspring regression, is more likely to underestimate than overestimate heritability. But point estimates of heritability in these diseases should probably be taken with a large dose of salt – even more than for heritability studies generally.
