quick recap

In my last post I derived the formulas for a model of prion protein degradation which I had previously simulated. The analytical solution matches the simulation (whew!) but the question remains: is this a good model?

This post will discuss two possible issues with the original model:

  1. It didn’t account for cell division
  2. It assumed that the PrPSc formation rate was independent of the concentration of PrPSc.

cell division

It has been pointed out that PrPSc accumulation in cell culture depends on three factors: the rates of conversion, degradation and cell division [Ghaemmaghami 2007]. My model only considered conversion and degradation. Is that wrong?

Before we get to PrPSc, let’s consider the simpler cases of PrP mRNA and PrPC. I’ll borrow Ghaemmaghami’s assumption that cells divide once every 24 hours, giving an exponential parameter ln(2)/24 = .029h-1, which I’ll call ξ (xi). If I consider the diluting effects of cell division, then my original expression for mRNA:

R'(t) = r - \lambda R(t)

Becomes:

R'(t) = r - (\lambda + \xi)R(t)

Hmm. Now all of a sudden, the steady state level of mRNA has gone from being Rsteady = r/λ to being Rsteady = r/(λ + ξ). The new steady state is λ/(λ+ξ) less than the old steady state. For the numbers considered here (mRNA half-life of 7h and cell division time of 24h), this works out to 77% of the original steady state value. Or viewed the other way around, you would have to transcribe RNA (λ + ξ)/λ – 1 = 29% faster in order to maintain the original steady-state level of mRNA.

And I don’t think that this is just a simple issue of having forgotten to account for there being more cells producing RNA as well. The above equation can be inferred to describe the steady state per cell (or per X number of cells), and even if daughter cells start producing mRNA as soon as cytokinesis is finished, they still don’t each have the same accumulation of previously-produced mRNA that the mother cell would if it hadn’t divided. Or to think of it a different way, mRNA production (r) is per diploid genome, and while two daughter cells have 4N ploidy / 2 cells = avg. 2N at the present moment, if you integrate over their recent history thhey haven’t always had as much DNA to go around.

But this, you’ll note, is a general issue that applies to all RNA transcripts and all proteins, not just PrP. Indeed, most proteins have a half-life on the order of several days, not hours [Price 2010], meaning they’d be much more depleted in dividing cells than PrP would be using the above numbers. Yet it seems unreasonable to suppose that all proteins and RNA are simply depleted in dividing cells.

There are several possible explanations which could resolve this issue. A better biologist than I would know which one is correct: perhaps RNA and protein synthesis are generally upregulated in interphase by enough to make up for the shortfall; perhaps continuously dividing cells are slightly smaller so that RNA and protein are not (as) depleted on a per volume or per surface area basis; and/or perhaps the answer is obscured by the fact that a huge number of genes change expression level during the cell cycle, such that the whole proteome is different and dynamic.

In any case, the empirical observation in [Ghaemmaghami 2007] was that the expression level of PrPC per μg of total protein was not different in dividing vs. stationary cells. I’ll assume the same is probably true of PrP mRNA as well.

What does this mean, then?

As one possible model of what’s going on, consider the case where:

R'(t) = (r + \xi) - (\lambda + \xi)R(t)

This could be held to represent an actual upregulation of PrP mRNA synthesis during cell division, or just a proportional upregulation due to other mRNAs being similarly depleted. Either way, the implication is that the same steady state is maintained as in stationary cells, but if you knock down transcription by half (0.5 * (r + ξ)) then the system reaches its new, knocked-down steady state slightly faster than it would otherwise. The assumptions in my last post dictated that a 50% reduction in transcription led to 76% of maximal inhibition after 24h; with cell division in the mix, that figure rises to 83%.

So that’s one possible interpretation. However it is also fair to ask whether the half-life estimates from the literature already include the effects of cell division. The citations for the mRNA and PrPC half-lives are [Pfeifer 1993] and [Borcheldt 1990] respectively. These studies involved radiolabeling and then extracting RNA or protein for slot blot or Western blot. Usually you standardize the mass of input material (e.g. protein) before doing a blot, in which case the measured half-lives probably already include effects of cell division; but if you just use the entire mass of RNA or protein from cell lysate, then you’re getting the rate of catabolism without the confounding effects of cell division. This is such a minute detail that I actually don’t see it noted anywhere in the materials and methods of these papers.

The standard error on these half-life measurements is probably huge anyway, to the point that the distinction doesn’t matter numerically. But it’s nice to have a model that’s conceptually correct. Here, I’m not sure which model that is.

Now, for PrPSc, the situation is different, for two reasons.

First, the reported half-life of PrPSc is longer than one cell division cycle (30h vs. 24h), so accounting for cell division makes a much bigger difference. ν/(ν + ξ) = .44, i.e. once cell division is accounted-for, the steady-state level of PrPSc is predicted to be only 44% of that in stationary cells. And sure enough, PrPSc accumulation in dividing cells is less than in stationary cells – standard errors are large, but the estimates is plausibly around the 44% value [Ghaemmaghami 2007].

The second reason is that, unlike mRNA and PrPC, whose production depends ultimately upon the number of copies of the genome (and therefore of the Prnp gene) available, PrPSc production depends upon the availability of PrPSc – which is diluted in cell divisions – to convert PrPC.

Or does it?

PrPSc availability

In my last post, I assumed that the rate of PrPSc production is proportional to the amount of PrPC available as substrate but does not depend on the amount of PrPSc available to do the converting.

That assumption is, of course, inconsistent with the physical reality that PrPSc-PrPC binding is required for prion conversion. Ghaemmaghami calls this the “heterodimer model”. In short:

The 1:1 stoichiometry here seems to indicate that the conversion rate should be proportional to both [PrPC] and [PrPSc]. (Note to non-biologists: square brackets mean “concentration of”).

Ghaemmaghami started from this assumption, proposing that:

\frac{dPrP^{Sc}}{dt} = k_{conversion}[PrP^C][PrP^{Sc}] - k_{degradation}[PrP^{Sc}] - k_{division}[PrP^{Sc}]

But he then discovered that [PrPC] appeared never to change, so he absorbed it into the constant:

\frac{dPrP^{Sc}}{dt} = k^*_{conversion}[PrP^{Sc}] - k_{degradation}[PrP^{Sc}] - k_{division}[PrP^{Sc}]

meaning that there ought to exist but one steady state, where:

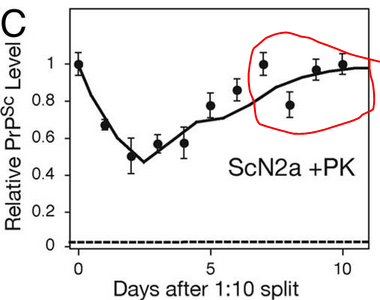
k^*_{conversion} = k_{degradation} + k_{division}

And yet he observed two steady states, one in dividing cells and one in stationary cells. The evidence for a steady state in stationary cells was that [PrPSc] appears to level off in the last few days of 10 days in culture without splitting, when the cells have pretty much grown to confluence, as shown in Fig 1C:

The conclusion of the paper was, then, that the rate of prion conversion must not depend on [PrPSc], or at least not on total [PrPSc]. Perhaps, instead, it depends on an infectious subset of PrPSc. Perhaps (and I’m extrapolating here) the “heterodimer” model isn’t always strictly correct in terms of stoichiometry – perhaps PrPSc often comes in larger fibrils or aggregates where new PrPC molecules can only be added to either end and not to the middle. Thus stationary cells might accumulate 2x more PrPSc than dividing cells and yet have barely more infectious material than dividing cells do. Alternately, it might be some other factor such as “Protein X” availability or space in lipid rafts which becomes the limiting reactant.

In any case, that’s a useful observation, because otherwise you end up with a very unstable system. Suppose, as Ghaemmaghami proposed, that [PrPC] is constant. Then:

\frac{dPrP^{Sc}}{dt} = (k^*_{conversion} - k_{degradation} - k_{division})[PrP^{Sc}]

If we just define a constant:

\varphi = k^*_{conversion} - k_{degradation} - k_{division}

Then the solution to the above differential equation is:

PrP^{Sc}(t) = PrP^{Sc}_0 e^{\varphi t}

From this equation, we can see that the initial quantity PrPSc0 will blow up exponentially without bound if φ > 0 and will be degraded to nothing if φ < 0. There is but one razor-thin unstable steady state at φ = 0 where PrPSc0 will be maintained indefinitely.

That’s actually not a bad model to fit the empirical observations of PrPSc‘s behavior in some experimental paradigms. For instance, human cell lines have never been successfully stably infected with prions – they always eventually clear the infection (φ < 0), while in vivo prion infection leads pretty much inevitably to an exponential rise in PrPSc and ultimately to death (φ > 0). So maybe there’s really something to this model! But in N2a cells, prions have been propagated stably for about 25 years now, since [Butler 1988], and no one’s going to convince me that this has been achieved simply by skating along the φ = 0 tightrope. It simply must be that, at least in this cell line, there is a more generous window of possible steady state values.

How, then, do we model the kinetics here? If we knock down mRNA by 50%, in my original simulation and equations that means, asymptotically, a 50% reduction in PrPSc. However, if this knockdown also reduces “PrPScinfectious” then it could potentially reduce PrPSc by more than 50%. Unfortunately, I’m not aware of any empirical observations that would allow us to quantify this relationship.

At a minimum, we could at least account for the effects of cell division. So I went back and took another look at the citation for a ~30h half life of PrPSc in N2a cells [Peretz 2001 (ft)]. Peretz never actually advances the 30h number, but rather cites [Borcheldt 1990] as evidence that the half-life is > 24h and notes that the time required for Fab D18 (an antibody fragment) to reduce PrPSc by 50% was 28h. As far as I can tell this experiment was done in continuously dividing cells, however, what was measured was total PrPSc rather than PrPSc per unit total protein, thus this half-life estimate would appear not to include the effects of cell division.

Therefore the best model would probably be one which assumes that the total clearance rate ν of PrPSc is equal to the measured half life ν0 = ln(2)/30h = .023h-1 plus the cell division parameter ξ = .029h-1. In order to accommodate the assumption that we’re beginning at steady state, then, we must also assume that the default value of β in untreated cells is equal to that new and improved value of ν. I’ve updated the gist from the last post to reflect this change. For now, I’ve also included ξ in the mRNA and PrPC clearance parameters λ and μ respectively, though it’s not clear whether or not this is correct.

I welcome any comments on this approach.