An introduction to Murcko fragments and structure-activity relationships using rcdk
Over the past few months I’ve learned a few basics of chemical informatics. I started with a few basics of how to use rcdk- that’s Rajarshi Guha‘s cheminformatics package for R [Guha 2007] - used these to compare the properties of CNS drugs vs. other drugs as well as antiprion compounds.
As a next step, this post will walk through me learning how to use rcdk to do a basic analysis looking for structure-activity relationships in a dataset. This is inspired in part by my recent discovery that there are two large datasets from anti-PrP screens in PubChem.
Wikipedia defines structure-activity relationship (SAR) as “the relationship between the chemical or 3D structure of a molecule and its biological activity”. In practice, if someone says that a high-throughput screening dataset “has an SAR” they mean that some of the hits from the chemical screen share common structural features that are probably responsible for their activity in the assay and provide a reasonable jumping-off point for further lead compound optimization. If a dataset is said to “have no SAR” that means the hits are a bunch of totally random compounds that look nothing like each other – a bad sign.
I didn’t manage to find a really elegant step-by-step SAR tutorial on the web, but from what I gather the process is basically two steps:
- break molecules into fragments
- look for fragments associated with bioactivity in the assay
Consider the most recent antiprion compound screen from the Prusiner lab [Silber 2013]. They screened ~50,000 compounds and found 970 hits after counterscreening. They found 20 molecular fragments that were enriched among these 970 hits, or put differently, they could group many of these 970 hits into 20 “leads”. Of the 20 leads, 14 were deemed worthy of followup, and so the top 2 hits from each lead category (i.e. top 2 hits containing each fragment) were selected for downstream experiments.
The fragments considered in that study were Murcko fragments. The inventors of this concept [Bemis & Murcko 1996] define a ring system as one or more rings sharing an edge, and a framework as the union of rings plus linker atoms connecting them. As far as I can tell, the term Murcko fragment is most often used to refer to “ring systems” as defined by Bemis and Murcko. (However, some of the fragments used in the Prusiner paper were ring systems plus “side chain atoms” and/or “linker atoms”).
fragments in rcdk
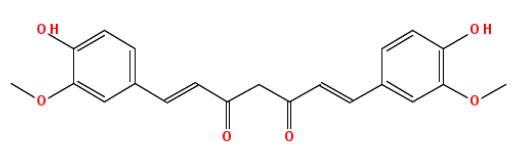
If you ask rcdk for Murcko fragments, it will give you ring systems in the molecule as well as frameworks in the molecule. Let’s try this with an example of an antiprion molecule we know well: curcumin. First some quick setup:
require(rcdk) # chemical informatics functionality in R
require(gap) # for qq plots later
options(stringsAsFactors=FALSE)
setwd('c:/sci/037cinf/analysis/sar/')
# plot molecules in R plot window instead of separate Java window
rcdkplot = function(molecule,width=500,height=500,marg=0,main='') {
par(mar=c(marg,marg,marg,marg)) # set margins to zero since this isn't a real plot
temp1 = view.image.2d(molecule,width,height) # get Java representation into an image matrix. set number of pixels you want horiz and vertical
plot(NA,NA,xlim=c(1,10),ylim=c(1,10),xaxt='n',yaxt='n',xlab='',ylab='',main=main) # create an empty plot
rasterImage(temp1,1,1,10,10) # boundaries of raster: xmin, ymin, xmax, ymax. here i set them equal to plot boundaries
}
Now, here’s what curcumin looks like:
curcumin = parse.smiles("O=C(\\C=C\\c1ccc(O)c(OC)c1)CC(=O)\\C=C\\c2cc(OC)c(O)cc2")[[1]]
rcdkplot(curcumin)
And rcdk finds that it contains exactly one Murcko ring system and one Murcko framework:
curc.frags = get.murcko.fragments(curcumin)
curc.frags
#[[1]]
#[[1]]$rings
#[1] "c1ccccc1"
#
#[[1]]$frameworks
#[1] "c1ccc(cc1)C=CCCCC=Cc2ccccc2"
png('curcumin.murcko.fragments.png',width=600,height=300)
par(mfrow=c(1,2))
rcdkplot(parse.smiles(curc.frags[[1]]$rings)[[1]])
rcdkplot(parse.smiles(curc.frags[[1]]$frameworks)[[1]])
dev.off()
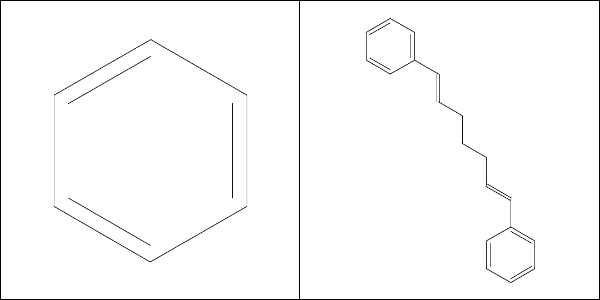
As expected, by Murcko’s definition, curcumin contains only one unique ring system (benzene, left). There’s also only one framework, defined as the rings plus the linker atoms in between (right). So far I’m happy with the defaults.
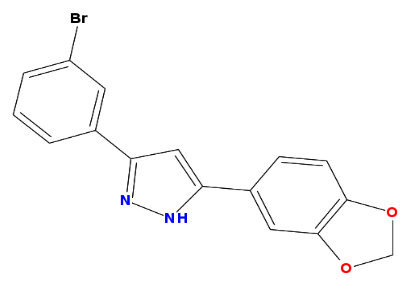
When I turn to a second example, anle138b, things get a bit more complicated.
anle138b = parse.smiles("C1OC2=C(O1)C=C(C=C2)C3=CC(=NN3)C4=CC(=CC=C4)Br")[[1]]
rcdkplot(anle138b)
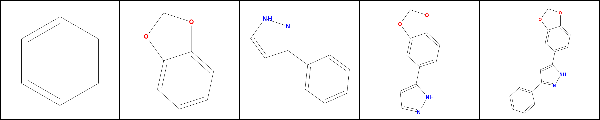
As you can see above, anle138b contains four unique ring systems: benzene, pyrazole, methylenedioxyphenyl, and C1OC=CO1 (the subset of the methylenedioxyphenyl without the benzene; not sure if this has a name). Yet, using the default settings, get.murcko.fragments recognizes only two:
anle138b.frags = get.murcko.fragments(anle138b)
anle138b.frags
# [[1]]
# [[1]]$rings
# [1] "c1ccccc1" "c1ccc2OCOc2(c1)"
#
# [[1]]$frameworks
# [1] "c1cccc(c1)c2n[nH]cc2" "c1n[nH]c(c1)c2ccc3OCOc3(c2)"
# [3] "c1cccc(c1)c2n[nH]c(c2)c3ccc4OCOc4(c3)"
png('anle138b.murcko.fragments.png',width=600,height=120)
par(mfrow=c(1,5))
rcdkplot(parse.smiles(anle138b.frags[[1]]$rings[1])[[1]])
rcdkplot(parse.smiles(anle138b.frags[[1]]$rings[2])[[1]])
rcdkplot(parse.smiles(anle138b.frags[[1]]$frameworks[1])[[1]])
rcdkplot(parse.smiles(anle138b.frags[[1]]$frameworks[2])[[1]])
rcdkplot(parse.smiles(anle138b.frags[[1]]$frameworks[3])[[1]])
dev.off()
It pulls out the benzene and methylenedioxyphenyl (from left: 1, 2) and then three frameworks (3, 4, 5). It turns out that rcdk does recognize pyrazole as a Murcko fragment, it’s just that pyrazole contains only 5 atoms, while the default minimum is 6. If we tweak this we can get pyrazole out as a ring:
anle138b.frags = get.murcko.fragments(anle138b,min.frag.size=3)
anle138b.frags[[1]]$rings
# [1] "c1ccccc1" "c1n[nH]cc1" "c1ccc2OCOc2(c1)"
Still, the C1OC=CO1 element is missing, not sure why that is. In any event, we’ve at least got something we can work with here.
toy SAR example
Before diving into any serious SAR for the anti-PrP datasets, I wanted to start with a toy example. The set of all FDA-approved drugs is a (regrettably) small dataset, and it contains 7 statins which share a well-characterized mechanism: they are all competitive inhibitors of HMG-CoA reductase. So as a toy example, let’s pretend that the US drugs were some random compound library that we screened to find compounds that reduce cellular cholesterol synthesis, and these 7 compounds were the hits.
First, let’s load up the structures of FDA-approved drugs and find the statins among them:
# load FDA drug list
drugs = read.table('/wp-content/uploads/2013/10/drugs.txt',
sep='\t',header=TRUE,allowEscapes=FALSE,quote='',comment.char='')
# remove those with no SMILES or with a really huge smiles
# otherwise R will hang on the macromolecules
drugs = drugs[nchar(drugs$smiles) > 0 & nchar(drugs$smiles) < 200,]
drug.objects = parse.smiles(drugs$smiles) # create rcdk IAtomContainer objects for each drug
# check that lengths are same
dim(drugs) # 1467 3
length(drug.objects) # 1467
statins = c("atorvastatin","fluvastatin","lovastatin","pitavastatin","pravastatin","rosuvastatin","simvastatin")
drugs[tolower(drugs$generic_name) %in% statins,] # check that the statins are in the drug list
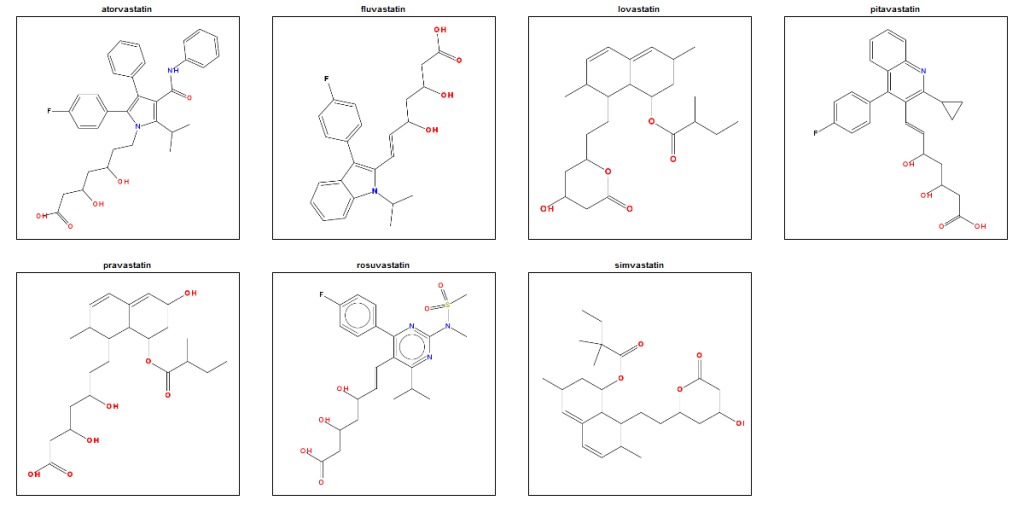
And now let’s take a look at the statin structures:
# examine statin structures
png('statin.structures.png',width=1200,height=600)
par(mfrow=c(2,4))
for (statin in statins) {
rcdkplot(drug.objects[tolower(drugs$generic_name) == statin][[1]],marg=2,main=statin)
}
dev.off()
To my eye, there are clearly some structural similarities between these molecules, presumably reflecting their similar biological activity. That suggests that perhaps this is a decent toy dataset to play around with. As a motivation for figuring out how to do an SAR, though, let’s remind ourselves that a fragment might be observed to recur in hit molecules either because (1) it’s important for their biological activity, or (2) because it was really common in the compound library you screened in the first place. To rule out (2), we’ll need to do some statistics to see if the common fragments in the statins are really enriched above their background frequency in the FDA-approved drugs.
For starters, let’s get a list of all the Murcko fragments that appear in any FDA-approved drug:
# get all murcko fragments
mfrags = get.murcko.fragments(drug.objects,min.frag.size=3)
# get a list of all possible fragments in any of these drugs
allfrags = unique(unlist(mfrags))
length(allfrags) # 2035
# get only the ring systems
allrings = unique(unlist(lapply(mfrags,"[[",1)))
length(allrings) # 556
If we consider rings and frameworks, there are 2035 fragments. If we only consider rings, there are 556. As a basic first foray into SAR, let's say I want to check each and every fragment to see whether it is significantly enriched in the "hits" from my assay (the statins). To do this, I'll want a big boolean matrix where the rows are drugs and the columns are fragments, and the cells are TRUE if the drug contains the fragment and FALSE if it does not. R fanatics, I could not for the life of me figure out a functional way (using apply) to convert mfrags into a matrix, so I'm going to fall back on a loop instead. Let me know if you have a genius solution. Otherwise, this works:
# convert to a matrix
mat = matrix(nrow=length(drug.objects), ncol=length(allrings))
for (i in 1:length(drug.objects)) {
mat[i,] = allrings %in% mfrags[[i]]$rings
}
Above I’ve decided to look for enrichment in only the rings. As an aside, if you want to consider both rings and frameworks, then it may be useful to collapse the internal structure of mfrags to just one vector per list item with this line of code:
# aside: if you want rings and frameworks thrown in together,
# do.call(c,mfrags[[1]]) will concatenate the elements of mfrags[[1]] into a vector
# lapply then does this to each element of the list
mfrags_all = lapply(mfrags,do.call,what=c)
At this point we’ve got all the 1s and 0s necessary to test for whether a fragment is associated with a compound being a “hit”. One way to think about this question is to ask whether a molecule’s status as having or lacking a fragment is independent of its status as being or not being a hit. That question can be asked using a Fisher exact test of independence (or, if your n were larger, a Chi squared test of independence):
is_statin = tolower(drugs$generic_name) %in% statins # is each drug a statin?
pvals = numeric(length(allrings)) # vector to hold p vals
for (j in 1:length(allrings)) { # iterate over rings
hasfrag = mat[,j] # does each drug contain this fragment?
contingency_table = table(data.frame(is_statin,hasfrag)) # 2x2 table
pvals[j] = fisher.test(contingency_table)$p.value # Fisher test of independence
}
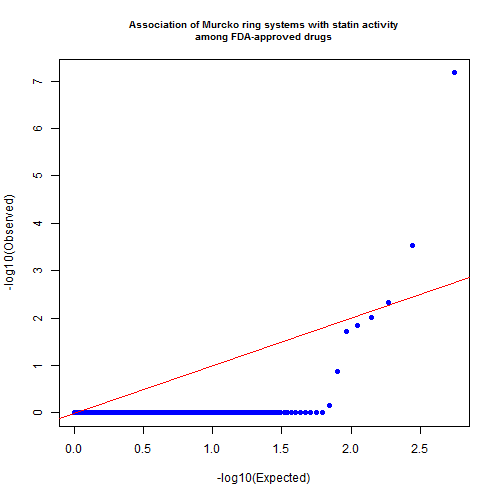
png('murcko.ring.statin.qqplot.png',width=500,height=500)
qqunif(pvals,pch=19,cex.main=.8,
main='Association of Murcko ring systems with statin activity\namong FDA-approved drugs')
dev.off()
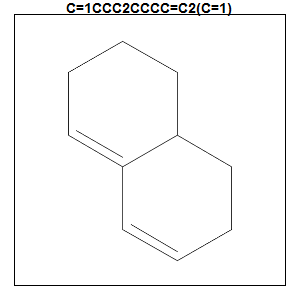
The QQ plot above suggests that there is indeed at least one fragment that is significantly enriched among the statins. What is it?
allrings[pvals < .000001]
# [1] "C=1CCC2CCCC=C2(C=1)"
# what statins contain it?
drugs$generic_name[is_statin & mat[,which(pvals < .000001)]]
# "Lovastatin" "Pravastatin" "Simvastatin"
# how many other drugs contain it
sum(!is_statin & mat[,which(pvals < .000001)])
# 0
rcdkplot(parse.smiles(allrings[pvals < .000001])[[1]],marg=1,main=allrings[pvals < .000001])
This fragment is present in 3 of the 7 statins, while it is present in 0 other drugs. That’s some pretty significant enrichment, with p = 6.7e-8.
That’s pretty cool, but let’s also go back and dissect what was done here. Note that p values are ordinarily supposed to be uniformly distributed between 0 and 1 under the null hypothesis, but Fisher’s exact test very often gives a p value of 1 as an answer, which makes the QQ plot above look a bit odd. QQ plotting implicitly assumes something along the lines of a Bonferroni correction for multiple testing correction – i.e. a p value is only significant if it’s more significant than the diagonal line would suggest based on the number of tests performed. If we had chosen 7 random compounds with no biological activity in common, and tested 556 ring fragments for enrichment in them, then we might expect that .05*556 ≈ 28 of them would be “significantly” enriched at p = .05, thus making this nominal significance not meaningful.
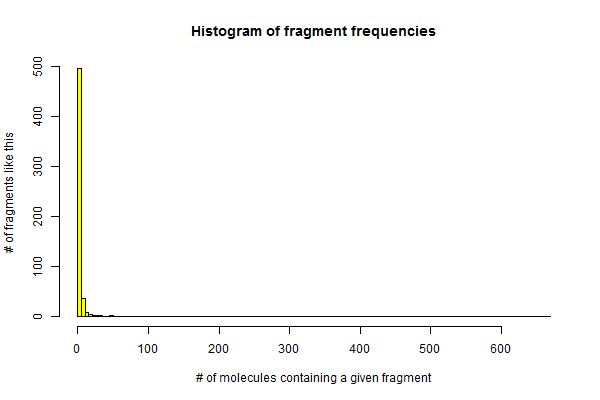
But this assumption is probably far too conservative for the conditions here. Fragments that occur in exactly one molecule in the entire drug collection could never be significantly enriched among the “hits”, and so they shouldn’t be considered to contribute to the multiple test burden. How big a problem is that? Are many fragments quite rare? Let’s look at a histogram of how frequent each of the 556 rings is in our drug collection:
hist(colSums(mat),col='yellow',breaks=100,
xlab='# of molecules containing a given fragment',
ylab='# of fragments like this',
main='Histogram of fragment frequencies')
Indeed, it looks a bit like an exponential distribution, with 351 of the 556 rings appearing in exactly 1 drug. There’s one wild outlier at the right – benzene appears in almost half of drugs.
sum(colSums(mat)==1)
# [1] 351
So the multiple testing burden isn’t nearly as bad here as I’ve assumed in my QQ plot above. In fact, only 8 fragments are even present at all in at least one hit:
sum(colSums(mat[is_statin,]) > 0)
# 8
So couldn’t we just test those and ignore the other 548 fragments? I’m interested in hearing reader’s arguments as to why yes or why no. In general I tend to err on the side of statistically conservative, so I’m going to say no, we still need to consider a larger multiple test burden than just 8 fragments. My argument is that under the null hypothesis, these are just 7 random molecules that turned up as “hits” due to noise in the assay, and the number of fragments present at an appreciable frequency in our chemical library bears on the likelihood of finding one fragment “significantly” enriched by chance.
Probably the most correct way to deal with multiple tests is to permute: repeatedly select a random subset of “hits” equal to the number of true hits, and see what the lowest p value you get is. Then if you want a 5% false discovery rate, select a p value where only 5% of the permutations have a lower p value. I won’t go into that level of analysis here in this post.
For now, at a minimum we can say that what I’ve done here is overly conservative and so the fragment is definitely significant, and the next few dots down the QQ plot might also be significant as well.
If I had considered all frameworks instead of just rings, the modeling task could get more complicated: if both a ring and a framework containing that ring are significant, then which is really important? Is the particular framework important or is just the ring important, and that’s the only or predominant framework within which the ring occurs? And so on.
which fragments are you looking at?
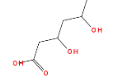
Getting away from the statistics questions, let’s address another issue with the result above: it is limited to ring systems as originally defined by Murcko. When I look at the statin structures in the graphic above, I see two other fragments that look interesting. One is this thing, which is in 5 of the 7 molecules:
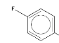
And another is fluorobenzene, which is present in 4 of the 7:
I’d really like to know if these fragments are involved in statins’ biological activity or not. My back-of-the-envelope guess is that they are significant, because in the histogram of fragment frequencies earlier, only one fragment (benzene) is very frequent, appearing in about half of drugs, while both fluorobenzene and this other thing appear in more than half of statins, suggesting enrichment
But I can’t actually count how many drugs contain fluorobenzene because, according to Murcko definitions, it’s not a fragment. The F is what’s dubbed a “side chain atom” [Bemis & Murcko 1996] and it is not considered in ring systems nor in frameworks.
To try to get at fluorobenzene, I turned to the other fragmenting system available in rcdk, get.exhaustive.fragments. After having R hang several times, I realized that this function is far more computationally intensive than get.murcko.fragments. I was finally able to run a single example to check performance:
start_time = Sys.time()
get.exhaustive.fragments(drug.objects[[which(drugs$generic_name=='Rosuvastatin')]],min.frag.size=3)
Sys.time() - start_time
# Time difference of 3.394177 mins
Computing the fragments for just one drug, Rosuvastatin, took > 3 minutes to find the 118 fragments of at least 3 atoms. Surprisingly, increasing the min.frag.size parameter only made matters worse: with min.frag.size = 7, this code took 12 minutes to produce 102 fragments. If Rosuvastatin is representative, then at that rate, it would take a few days to compute exhaustive fragments on the whole US drug collection.
That’s certainly an option, though if I have to turn to a compute farm just to do one toy example for my blog, then I’ll be a bit worried about how much compute time it will take to do any real analysis.
Another issue is that even exhaustive fragments are limited to contiguous fragments. Might biological activity sometimes be due to a discontinuous property of the molecule? I found it interesting that in the Prusiner lab screening paper cited above [Silber 2013], the SAR focused on contiguous fragments but the manual examination of the compounds by the medicinal chemists led to some “discontinuous” observations (my bold):
Upon closer examination of the hits across different chemical leads, several trends became evident. A conjugated aromatic or heteroaromatic ring system was prominent in all lead structures. This ring system is comprised of more than two aryl or heteroaryl groups joined in a fused or linear fashion. In the case of linear aromatic systems, two aromatic rings can be linked directly via a carbon-carbon bond or a linker such as an amide or double bond. Further analysis revealed that compounds with better potency (<1 μM) were from leads having core structures possessing a flat coplanar or near coplanar conformation…
The bolded logic is vaguely reminiscent of a regular expression of sorts: (hetero)?aryl((carbon-carbon|amide|double bond)(hetero)?aryl){1,}. This makes me wonder if it would be possible to implement regex-like logic on molecular structures to find discontinuous patterns that are enriched among assay hits. Of course, a vast number of potential regular expressions will match any given string, and so the concept of simply “fragmenting” a molecule would not apply – one would need to be very smart about choosing regexes to bother to try to match.
conclusion
All of the code from this post is available in this GitHub Gist. This was the most basic imaginable example just to get my head around how to use fragments in SAR. Hopefully now I’ve got enough of an idea to start trying to apply this to real datasets and learn more things as I go.